Rechengesetze
Punkt vor Strich
Eine der wichtigsten Regeln in der Mathematik ist die "Punkt vor Strich" Regel. Damit ist gemeint, dass wenn in einer Rechnung ein Punkt (Mal und Geteiltdurch) und ein Strich (Plus und Minus) vorkommen, und diese nicht durch eine Klammer abgetrennt sind, man erst multipliziert/dividiert und dann erst addiert/subtrahiert.
Beispiel:
4+2·3=4+6=10
Weitere Beispiele:
Gesetze bei Addition
Kommutativgesetz (Vertauschungsgesetz) bei Addition
Dieses besagt, man darf bei Plus die beiden Summanden vertauschen, wie man will, es kommt immer dasselbe raus. WICHTIG: Das gilt nur für Addition, also Plus, nicht bei Subtraktion (Minus)!!
3+6=6+3
2+1=1+2
Assoziativgesetz (Verbindungsgesetz) bei Addition
Das besagt, dass wenn man eine Addition hat (gilt wieder NICHT bei Subtraktion), man beliebig Klammern um einzelne Summanden machen darf und es kommt dasselbe raus.
(3+6)+5=3+(6+5)
(1+2)+3=1+(2+3)
Gesetze bei Multiplikation
Kommutativgesetz (Vertauschungsgesetz) bei Multiplikation
Dieses besagt, man darf bei der Multiplikation die beiden Faktoren vertauschen, wie man will, es kommt immer dasselbe raus. WICHTIG: Das gilt nur für die Multiplikation, also Mal, nicht bei Division (Geteilt-durch)!!
6·5=5·6
2·1=1·2
Assoziativgesetz (Verbindungsgesetz) bei Multiplikation
Das besagt, dass wenn man eine Multiplikation hat (gilt wieder NICHT bei Division), man beliebig Klammern um einzelne Summanden machen darf und es kommt dasselbe raus.
(3·6)·5=3·(6·5)
(1·2)·3=1·(2·3)
Minus mal Minus ergibt Plus
Wenn ihr zwei negative Zahlen multipliziert, ergibt es eine positive Zahl. Ist dagegen nur eine Zahl negativ, ergibt es eine negative Zahl.
(-4) · (-2) = 8
(-2) · 3 = -6
Distributivgesetz (Verteilungsgesetz)
Dieses besagt, man darf, wenn es möglich ist, immer ein- und ausklammern, vorausgesetzt man macht es mit den Regeln mehr zum Thema hier: Ausklammern und Ausmultiplizieren.
5·(3+5)=5·3+5·5
Klammer Rechenregeln
Ausführliche Erklärungen zu Klammer Rechenregeln findet ihr im Artikel zur Klammerrechnung. Hier eine kurze Zusammenfassung.
- Wenn ihr eine Klammer habt, müsst ihr immer erst das Innere der Klammer ausrechnen oder diese auflösen. Es gilt die Regel "Klammer zuerst"! (sogar vor "Punkt vor Strich") (mehr zum Thema hier: Ausklammern und Ausmultiplizieren)
2·(3+5)=2·8=16
2·(3-1)-(3-1)=2·2-2=2
- Ist ein Minus vor der Klammer, müsst ihr dieses in die Klammer "verrechnen", bevor ihr diese auflöst.
-(2+3)=-2-3=-5
10+2-(3+2)=10+2-3-2=7
- Klammer richtig auflösen, wenn ein Faktor davor steht. Dazu multipliziert ihr jeden Faktor bzw. Zahl in der Klammer mit dem Faktor, der davor steht. (mehr zum Thema hier: Ausklammern und Ausmultiplizieren)
5·(2+3)=5·2+5·3
- Wenn ihr eine Klammer mal eine andere Klammer verrechnet, müsst ihr jeden Summanden einer Klammer mit jedem Summanden der anderen Klammer mal nehmen:
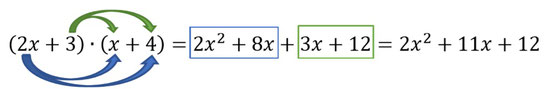
Aufgaben zu den Rechengesetzen
Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Übungsblätter downloaden und ausdrucken. Lösungen zu den Aufgaben findet ihr dort ebenfalls:
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.


