Wurzel einer Zahl
In diesem Beitrag geht es um die Wurzel. Es handelt sich dabei um die Umkehrung der Potenz.
Eine Wurzel sieht so aus:

- a ist der Radikand
-
- davon wird die "Wurzel gezogen"
- a darf nicht negativ sein! Man darf nur von positiven Zahlen die Wurzel ziehen.
- b ist der Wurzelexponent
-
- diese Zahl sagt, welche Wurzel gezogen wird, also ob die 2., 3., ...
- √ ist die Wurzel. Alles was unter ihr steht wird radiziert (von dem wird die Wurzel gezogen).
Was bringt uns das?
Die Wurzel hilft euch herauszufinden, was man hoch b nehmen musste, um a zu erhalten. Auch um Potenzgleichungen zu lösen, ist die Wurzel sehr wichtig. Sie bedeutet umgeschrieben Folgendes:

Beispiel

Quadratwurzel
Eine besonders wichtige und häufige Wurzel ist die Quadratwurzel. Das ist eine Wurzel, bei der der Exponent 2 ist. Für diese gibt es auch eine vereinfachte Schreibweise, ihr dürft dann einfach den Wurzelexponenten an der Wurzel weglassen, das steht dann auch für die Quadratwurzel:

Eigenschaften einer Wurzel
- Sind der Wurzelexponent und der Exponent beim Radikanden gleich, löst sich die Klammer auf (geht natürlich nicht nur bei hoch 2):

- Wird die Wurzel mit derselben Zahl potenziert, wie der Wurzelexponent, fällt die Wurzel ebenfalls weg (geht natürlich nicht nur bei hoch 2):

- Man kann eine Wurzel auch umschreiben, indem man den Radikanden hoch den Kehrbruch des Wurzelexponenten nimmt (geht natürlich nicht nur bei hoch 2):
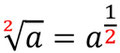
Wurzelrechenregeln
Alle Rechenregeln zu den Wurzeln einfach erklärt findet ihr in einem separaten Artikel:
Passende Themen:
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.



