Lage von Ebenen bestimmen
Für die Lage einer Ebene zu einer Ebene gibt es 3 Möglichkeiten:
-
Die Ebenen sind identisch
-
Die Ebenen sind parallel
-
Die Ebenen schneiden sich
Möchtet ihr die Lage einer Ebene zu einer Ebene bestimmen, geht ihr Schritt für Schritt so vor (sehr ähnlich der Lage von Ebene zu Gerade):
- Stellt sicher, dass die eine Ebene in Koordinatenform ist und die andere in Parameterform, wenn nicht müsst ihr diese noch umformen. Wie das geht, findet ihr im Artikel zum Umformen von Ebenengleichungen.
- Setzt die Ebenengleichung in Parameterform in die Ebenengleichung in Koordinatenform für die x Werte ein (dabei ist die erste Zeile der Ebenengleichung x1, die zweite Zeile x2, die 3. Zeile x3. (Im Beispiel könnt ihr euch dies noch genauer anschauen). Dies ist genauso wie bei der Lage von Ebene zu Gerade.
- Löst die Gleichung, die ihr so erhaltet, dann gibt es 3 Möglichkeiten, was herauskommt:
- Ihr erhaltet eine Lösung, die nicht von λ und μ abhängt und wahr ist. Also zum Beispiel 1=1 oder 4=4. Dann sind die Ebenen identisch.
- Ihr erhaltet eine Lösung, die nicht von λ und μ abhängt und falsch ist. Also zum Beispiel 2=1 oder -2=2. Dann sind die Ebenen parallel.
- Ihr erhaltet eine Lösung, die λ und/oder μ enthalten. Zum Beispiel λ=μ+1. Dann schneiden sich die Ebenen. Um dann die Schnittgerade zu erhalten, löst ihr das Ergebnis eurer Gleichung von darüber nach μ auf und setzt das dann für μ in die Ebenengleichung in Parameterform ein. Diese müsst ihr nur noch ausmultiplizieren und ihr seid fertig. (Im Beispiel Genaueres)
Beispiel zur Bestimmung der Lage von Ebenen
Habt ihr zwei Ebenen gegeben, zum Beispiel diese:
- Dann bestimmt ihr zuerst die einzelnen x-Werte, indem ihr diese aus den Zeilen der Ebene in Parameterform ab. Die erste Zeile ist x1, die zweite Zeile x2 und die dritte Zeile x3:
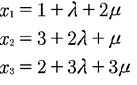
- Diese Werte setzt ihr dann in die Koordinatenform der anderen Ebene ein (also das was ihr für x1 habt für x1 einsetzen usw) und berechnet das Ergebnis. Löst dabei nach einer Variablen auf (egal nach welcher) falls sie nicht wegfallen:
- Es können die oben genannten Ergebnisse aus Punkt 3 rauskommen. Hier habt ihr eine Lösung mit den Unbekannten, also schneiden sich die Ebenen. Um die Schnittgerade zu bestimmen, setzt ihr einfach für die Unbekannte, nach der ihr oben aufgelöst habt, die Lösung von gerade in die Parameterform der Ebene ein und rechnet es aus, das ist dann eure Schnittgerade (ihr seht, es wurde für μ die Lösung von darüber in die Parameterform eingesetzt und ausgerechnet).:
Wie ihr seht, können ganz schräge Werte für die Schnittgerade rauskommen.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
