Mitternachtsformel
Die Mitternachtsformel ist eine Formel um quadratische Gleichungen der Form 0=ax2+bx+c lösen zu können.


Habt ihr eine Gleichung in dieser Form, dann setzt ihr a, b und c in folgende Formel ein.
Dabei ist:
- a immer die Zahl vor dem x hoch 2.
- b immer die Zahl vor dem x (ohne hoch 2)
- c immer die Zahl ganz ohne x
Das ± bedeutet, dass ihr die Formel zweimal rechnen müsst, nämlich einmal mit – und einmal mit +. Es kann nämlich bei quadratischen Gleichungen zwei Lösungen geben. Beispiele findet ihr weiter unten.
Wichtiger Hinweis: Sollte unter der Wurzel etwas negatives rauskommen, dann hat diese Gleichung keine Lösung. Es gibt also keinen Wert für x, wofür die Gleichung dann 0 ergibt.
Beispiel: Mitternachtsformel anwenden
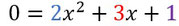
Ihr habt diese Gleichung gegeben.
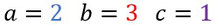
Bestimmt jetzt a, b und c.

Setzt die Werte für a, b und c in die Mitternachtsformel ein und vereinfacht so weit wie möglich.

Jetzt berechnet ihr es einmal für + und einmal für –. Nun habt ihr beide mögliche Lösungen. Übrigens ist es egal, ob bei x1 oder x2 minus/plus gerechnet wird.
2. Beispiel: Mitternachtsformel berechnen
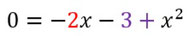
Ihr habt diese Gleichung gegeben.
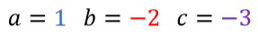
Bestimmt a, b und c. Aber aufpassen, nicht von der Reihenfolge in der Gleichung verwirren lassen!

Setzt a, b und c in die Formel ein und vereinfacht soweit wie möglich.
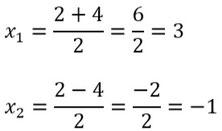
Jetzt rechnet ihr es einmal für + und einmal für – aus. Nun habt ihr beide mögliche Lösungen. Übrigens ist es egal, ob bei x1 oder x2 minus/plus gerechnet wird.
Aufgaben zur Mitternachtsformel
Hier einige Aufgaben zum Üben der Mitternachtsformel. Klickt auf einblenden, um die Lösung zu sehen.
| 5x2+x-4=0 | Einblenden | |
|
Lösung:
|
||
| 2x2-4x+2=0 | Einblenden | |
|
Lösung:
|
||
| 7x2-14x=0 | Einblenden | |
|
Lösung:
|
||
| -2x2-9x+5=0 | Einblenden | |
|
Lösung:
|
||
| 2x2+3x-2=0 | Einblenden | |
|
Lösung:
|
||
| 5x2-1x-4=0 | Einblenden | |
|
Lösung:
|
||
| 8x2-4x-4=0 | Einblenden | |
|
Lösung:
|
||
| -3x2-6x+9=0 | Einblenden | |
|
Lösung:
|
||
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.



