Achsen- und Punkt-/Drehsymmetrie
Achsensymmetrie
Achsensymmetrie bedeutet, dass eine Figur eine Symmetrieachse hat, was bedeutet, dass ein Objekt links und rechts von dieser Achse identisch ist. Würde man nun die Figur an dieser Achse "umklappen", würden die beiden Hälften deckungsgleich sein.
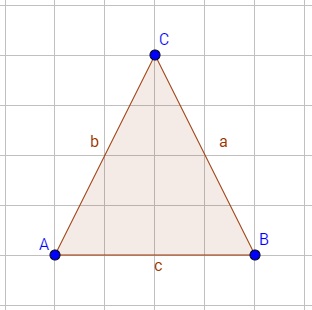
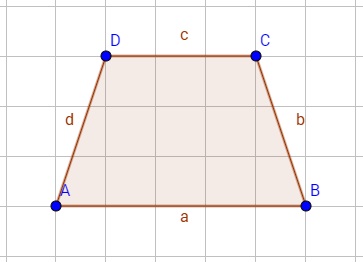
Hier seht ihr ein Beispiel, für eine achsensymmetrische Figur. Die gestrichelte Linie ist dabei die Symmetrieachse. Links und rechts von dieser Achse ist die Figur identisch, weshalb sie achsensymmetrisch ist.
Beispiele für Achsensymmetrie
Punktsymmetrie/Drehsymmetrie
Punktsymmetrie bedeutet, dass die Punkte einer Figur an einem Spiegelpunkt gespiegelt werden und dabei die Figur gleich bleibt. Sie wird auch häufig als Drehsymmetrie bezeichnet, da man die Figuren auch um 180° drehen kann, was einer Punktspiegelung gleich kommt, und wenn dann dasselbe raus kommt, ist die Figur drehsymmetrisch.
Hier seht ihr eine punktsymmetrische Figur, wenn alle Punkte am Spiegelpunkt gespiegelt werden, kommt wieder exakt dieselbe Figur raus. Genauso, wenn man sie um 180° um sich selbst dreht.
Beispiele für Punktsymmetrie bzw. Drehsymmetrie
Ein Parallelogramm ist punktsymmetrisch bzw. drehsymmetrisch.
Ein Rechteck ist punktsymmetrisch bzw. drehsymmetrisch.
Ein Quadrat ist punktsymmetrisch bzw. drehsymmetrisch.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
