Polynomdivision Schritt für Schritt mit Beispiel
Die Polynomdivision ist eine Methode, mit welcher sich beispielsweise Nullstellen von Polynomen leichter berechnen lassen und womit auch Asymptoten von Polynomfunktionen bestimmt werden können. Dieses Vorgehen erklären wir euch anhand eines Beispiels. Dabei führt ihr immer wieder dieselben 4 Schritte aus, bis ihr fertig seid.
Ihr habt beispielsweise diese Polynomdivision:
Dann geht ihr Schritt für Schritt so vor:
1. Teilt das x (aus eurem Polynom (x+1)) durch das x ganz links in eurem eigentlichen Polynom. Das Ergebnis schreibt ihr hinter das = :
2. Multipliziert das Ergebnis dann mit dem Polynom (x+1). Schreibt das Ergebnis in Klammern und einem Minus davor unter euer
Polynom:
3. Subtrahiert die Teile, welche nun untereinander stehen, dabei dürft ihr nicht vergessen, dass das Minus vor der Klammer steht! Das Ergebnis schreibt ihr darunter. Dann zieht ihr den nächsten Teil vom Polynom runter (also das Glied, welches als nächstes im Polynom steht):
4. Das macht ihr jetzt alles noch mal, nur dass ihr mit dem, was ihr unter dem Polynom geschrieben habt, rechnet.
1. Also wieder das x durch das was ganz links steht teilen und das Ergebnis hinten dran addieren:
2. Dann wieder das Ergebnis mal das Polynom (x+1) nehmen und das, was raus kommt, darunter mit einem Minus schreiben:
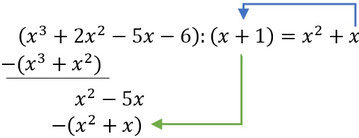
3. Wieder die beiden untereinander stehenden Terme subtrahieren, das Ergebnis darunter Schreiben. Dann zieht ihr das nächste Glied aus dem Polynom runter:
4. Das macht ihr jetzt alles noch mal ab Schritt 4 nur, dass ihr mit dem, was ihr runter geschrieben habt, rechnet.
1. Also wieder das x durch das was ganz links steht teilen und das Ergebnis hinten dran addieren:
2. Dann erneut das Ergebnis mit dem Polynom (x+1) multiplizieren und das Ergebnis mit einem Minus darunter schreiben.
3. Die beiden untereinander stehenden Terme voneinander abziehen, das Ergebnis darunter Schreiben:
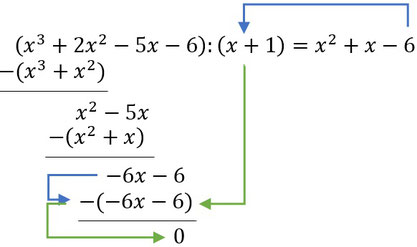
Sobald ihr kein weiteres Glied mehr runterziehen könnt, seid ihr fertig. Falls ein Rest übrig bleibt, findet ihr weiter unten, was dann zu tun ist. Mit dem Ergebnis könnt ihr, z.B. mit der Mitternachtsformel, die restlichen Nullstellen bestimmen.
Bleibt Rest übrig (z.B. bei Asymptoten berechnen)
Sollte ein Rest übrig bleiben, dann müsst ihr diesen noch durch euer Nullstellenpolynom teilen und hinten dran addieren. Das nennt man dann Restterm. Dann seid ihr auch fertig. Hier ein Beispiel dazu:
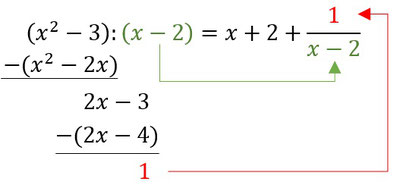
Nullstellen berechnen mit der Polynomdivision
Benutzt ihr die Polynomdivision zum Berechnen von Nullstellen, dann ist oft der Term, durch den das Polynom geteilt wird, nicht gegeben. Ihr müsst dann durch Probieren eine Nullstelle finden, denn man führt die Polynomdivision mit dem Nullstellenpolynom durch. Dabei wird x minus den x-Wert der Nullstelle genommen.
- Zum Beispiel wenn eine Nullstelle bei 1 ist, würde das Nullstellenpolynom so aussehen: (x-1)
- Bei einer Nullstelle bei -3 würde es so aussehen: (x+3)
Immer so, dass Null rauskommen würde, wenn man die Nullstelle einsetzt. Dann führt ihr die Polynomdivision durch, indem ihr das Polynom, für welches ihr die Nullstellen erfahren möchtet, durch das Nullstellenpolynom teilt (geht dann so vor, wie in den vorherigen Seiten beschreiben). Habt ihr dann das Ergebnis, müsst ihr von diesem die Nullstellen bestimmen (z.B. mit der Mitternachtsformel, oder falls es immer noch ein Polynom von einem Grad größer als 2 ist, noch mal die Polynomdivision durchführen). Diese Nullstellen sind dann (zusammen mit der vom Nullstellenpolynom) die Nullstellen des Polynoms.
Aufgaben zur Polynomdivision
Hier sind Aufgaben die ihr Lösen, oder einfach anschauen könnt. Klickt auf Einblenden, um die Lösung zu sehen:
| (2x3+4x2-2x-4):(x-1)= | Einblenden | |
| (x3-2x2-5x+6):(x-1)= | Einblenden | |
Aufgaben selbst erstellen
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
