Vierfeldertafel
Die Vierfeldertafel ist neben dem Baumdiagramm eine andere Möglichkeit, Wahrscheinlichkeiten darzustellen und vereinfacht das Ausrechnen dieser.

- P(A) ist die Wahrscheinlichkeit für A
- P(A∩B) ist die Wahrscheinlichkeit, dass A und B zutreffen
- A ist das Ereignis A (A "Strich" ist das Gegenereignis, also das Gegenteil von A)
Hier seht ihr den Aufbau einer Vierfeldertafel.
- oben in der ersten Zeile und in der Spalte ganz links sind die beiden Ereignisse und Gegenereignisse eingetragen (Strich über dem Gegenereignis)
- die 4 mittleren Felder sind die jeweiligen "Undwahrscheinlichkeiten" der Ereignisse also, dass z.B. Ereignis B und A zutreffen.
- die untere Zeile und die rechte Spalte sind die Wahrscheinlichkeiten der einzelnen Ereignisse, z.B. das A zutrifft.
- ganz unten rechts steht immer 100%
- es können auch die Häufigkeiten, anstatt der Wahrscheinlichkeiten, eingetragen werden, also wie häufig etwas vorgekommen ist, ganz unten rechts steht die Gesamtanzahl.
Rechnen mit der Vierfeldertafel

Hier seht ihr, wie in einer Vierfeldertafel gerechnet wird. Wenn man die Zeilen addiert, erhaltet ihr die Wahrscheinlichkeit ganz rechts. Addiert ihr die Spalten, erhaltet ihr die Wahrscheinlichkeit ganz unten.
Beispiel: Vierfeldertafel ausfüllen
30 Schüler einer Schulklasse schreiben einen Mathetest. Darunter sind 15 Schüler, die immer die Hausaufgaben machen. Insgesamt
bestehen 12 Schüler den Test. 9 Schüler, welche regelmäßig die Hausaufgaben machen, haben am Ende bestanden.
Mit welcher Wahrscheinlichkeit hat ein Schüler den Test nicht bestanden und hat keine Hausaufgaben gemacht?
Lösung:
- Überlegt euch die Ereignisse. Hier gibt es bestanden, nicht bestanden, machen Hausaufgaben und machen keine Hausaufgaben.
- Schaut, welche Ereignisse ihr gegeben habt:
-
- P(M∩B): Wie viel Prozent Hausaufgaben machen und bestanden haben
-
P(M): Wie viel Prozent Hausaufgaben machen (M steht für machen)
-
P(B): Wie viel Prozent insgesamt bestehen (B steht für bestehen)
- Berechnet die Wahrscheinlichkeiten die ihr wisst. Also von 30 Schülern machen ja 15 Schüler Hausaufgaben, also 50%. Ihr teilt immer die gesamte Anzahl von dem, was zutrifft, durch die Gesamtanzahl an Schülern. Hier gehts zur Kombinatorik.
-
- z.B. die Wahrscheinlichkeit dafür, dass ein Schüler Hausaufgaben macht und gleichzeitig bestanden hat, ist folgendes: Ihr teilt die Anzahl an Schülern, die Hausaufgaben machen und bestanden haben, durch die Gesamtanzahl an Schülern, also 9:30=0,3=30%
- Füllt alles in die Vierfeldertafel ein, was ihr wisst:

Hier seht ihr die eingetragenen Wahrscheinlichkeiten, dabei steht...
- B für bestanden und
- M für machen Hausaufgaben,
- die Gegenwahrscheinlichkeiten sind dann "nicht bestanden" und "machen keine Hausaufgaben".
- Nun berechnet ihr die restlichen Werte, so wie oben gezeigt wurde:
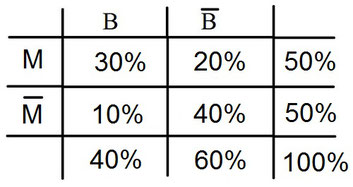
Nun kennt ihr alle Wahrscheinlichkeiten. Also haben 40% der Schüler keine Hausaufgaben gemacht und den Test nicht bestanden. (Guckt die Wahrscheinlichkeit an, welch bei "machen keine Hausaufgaben" und "nicht bestanden" in der Vierfeldertafel steht.)
Alternative: Häufigkeit in der Vierfeldertafel
Anstatt von Wahrscheinlichkeiten kann man auch die absoluten Häufigkeiten in die Vierfeldertafel eintragen, mit dem Beispiel von darüber sieht es dann so aus:

Wie ihr seht, werden die Anzahlen, wie viele Schüler jeweils zu einem dieser Ereignisse passen, eingetragen. Wenn ihr jetzt hier alle Werte durch die Gesamtanzahl an Schülern (also 30) teilt, erhaltet ihr die Wahrscheinlichkeiten!
Passende Themen
- Anzahl der Möglichkeiten ausrechnen (Kombinatorik)
- Absolute und Relative Häufigkeit
- Baumdiagramm
- Bedingte Wahrscheinlichkeit
- Ergebnis, Mächtigkeit und Ergebnismenge
- Ereignis, Mächtigkeit und Ereignismenge
- Laplace Experiment
- Mengenschreibweisen und Symbole
- Prozentrechnung
- Stochastische Unabhängigkeit
- Zufallsexperiment

