Logarithmus und seine Rechenregeln
Der Logarithmus ist die Umkehrung vom Potenzieren. Dies ist ein wichtiges Thema, hier findet ihr eine Übersicht zu allem Wichtigen, erst mal wie der Logarithmus definiert ist:
logba=x → bx=a
Gesprochen heißt das: "Logarithmus von a zur Basis b". Dabei ist...:
- b die Basis
- a der Wert, welcher rauskommt, wenn man b hoch x nimmt
- x der Exponent
Wie funktioniert der Logarithmus?
Den Logarithmus braucht ihr, um Gleichungen zu lösen, in denen der Exponent unbekannt ist, denn sonst könntet ihr diese Gleichungen nicht lösen. Ihr wollt zum Beispiel dieses x berechnen:
2x=1024
Das herauszufinden ist an sich nicht so leicht, aber ihr könnt es ja mit dem Logarithmus lösen, dieser ist nämlich dann:
2x=1024 -> log21024=x
x=10
Beispiele:
- log28=3 → 23=8
- log39=2 → 32=9
- log33=1 → 31=3
Aufgaben mit Beispielen:
Hier sind Aufgaben, die ihr rechnen oder einfach angucken könnt. Klickt auf einblenden, um die Lösung zu sehen:
| 2x=16 | Einblenden | |
|
Lösung: → log216=4 -> x=4 |
||
| 2x+2=10 | Einblenden | |
|
Lösung: 2x+2=10 |-2 2x=8 -> log28=3 -> x=3 |
||
| log3x=3 | Einblenden | |
|
Lösung log3x=3 → 33=x → x=27 |
||
| 5x=25 | Einblenden | |
|
Lösung: → log525=2 -> x=2 |
||
| 3x+4=13 | Einblenden | |
|
Lösung: 3x+4=13 |-4 3x=9 -> log39=2 -> x=2 |
||
| log5x=2 | Einblenden | |
|
Lösung: log5x=2 → 52=x → x=25 |
||
Dekadischer Logarithmus
So wird jeder Logarithmus genannt, welcher als Basis die 10 hat. Diesen braucht ihr nicht nur bei Exponenten mit der Basis 10, sondern auch, um andere Logarithmen im Taschenrechner auszurechnen, da die meisten Taschenrechner keine Taste für alle Logarithmen haben. Meist wird der dekadische Logarithmus mit lg abgekürzt.
log10(a) = lg(a)
Natürlicher Logarithmus
Der sogenannte natürliche Logarithmus ist ein Logarithmus mit Basis e (eulersche Zahl). Dies ist eine besondere unendlich nicht periodische Zahl (wie π auch). Dieser Logarithmus hat auch eine spezielle Abkürzung:
loge(x) = ln(x)
Logarithmus im Taschenrechner eintippen
Um einen Logarithmus im Taschenrechner einzutippen, welcher weder der dekadische noch natürliche Logarithmus ist, also z.B. mit der Basis 2, benötigt ihr den dekadischen oder natürlichen Logarithmus. Ihr teilt dann den natürlichen/dekadischen Logarithmus der Zahl, durch den natürlichen/dekadischen Logarithmus der Basis. Dabei ist es egal, ob ihr den natürlichen oder dekadischen Logarithmus nehmt, es muss nur immer derselbe durcheinander geteilt werden:
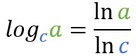
Beispiele:


Logarithmusgesetze - Rechenregeln
"Produkt wird zur Summe"
logb(a·c)=logba+logbc
Beispiel:
log3(x·9)=log3x+log39
Diese Regel besagt, dass wenn in der Klammer beim Logarithmus ein Produkt steht, man jeweils den Logarithmus für beide Faktoren einzeln berechnen kann und diese dann addiert.
| log2(x·4) | Einblenden | |
|
Lösung: → log2x+log24 → log2x+2 |
||
| log3(9x) | Einblenden | |
|
Lösung: → log3x+log39 → log3x+2 |
||
"Division wird zur Subtraktion"

Beispiel:
log3(x/9)=log3x-log39
Diese Regel besagt, dass wenn in der Klammer eine Division, bzw. ein Bruch steht, man es wie beim Produkt machen kann, nur mit einem Minus.
| log3(x/27) | Einblenden | |
|
Lösung: → log3x-log327 → log3x-3 |
||
| log2(8/x) | Einblenden | |
|
Lösung: → log28-log2x → 3-log2x |
||
"Exponenten kann man vorziehen"
logban=n·logba
Beispiel:
log392=2·log39
Diese Regel besagt, dass wenn die Basis (a) einen Exponenten hat, man diesen vor den Logarithmus ziehen kann.
Division mit gleicher Basis

Beispiel:
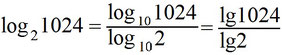
Teilt man zwei Logarithmen mit gleicher Basis, dann kann man es zu einem Logarithmus von „a“ zur Basis „c“ umwandeln.
Basis und logarithmierter Wert gleich
logaa=1
Beispiel:
log33=1
Ist das, was logarithmiert wird, dasselbe wie die Basis, ergibt es IMMER 1.
Denn: log33=1 → 31=3
Eins logarithmiert ist immer 0
loga1=0
Beispiel:
log51=0
Wird die 1 logarithmiert, kommt IMMER 0 raus.
Denn: log31=0 → 30=1
