Ableitung - Eine Übersicht

Hier findet ihr alles zur Ableitung einfach erklärt. Klickt auf ein Thema um direkt dort hin zu scrollen:

Allgemeines zur Ableitung
Wie erkennt und kennzeichnet man Albeitungen?
Wie funktioniert die Ableitung?
Ableitungsregeln
mehrfache Ableitung und ihre Bedeutungen

Allgemeines zur Ableitung

Wie erkennt man, bzw. kennzeichnet man sie?

Wenn eine Funktion abgeleitet wurde, kennzeichnet man es durch einen Strich nach dem Namen der Funktion:

f´(x) -> 1. Ableitung
f´´(x) -> 2. Ableitung (wurde erst einmal abgeleitet und dann wurde die Ableitung noch mal abgeleitet)
f´´´(x) -> 3. Ableitung
....

Für die Ableitung gibt es noch weitere Schreibweisen, außer f´(x), die aber dasselbe bedeuten:

Schreibweisen der Ableitung in einer Übersicht erklärt.

Wie funktioniert die Ableitung?

Hier seht ihr, wie die Ableitung für verschiedene Funktionen funktioniert mit jeweils einem Beispiel:

Funktion	Ableitung	Beispiel
f(x)=c	f´(x)=0	y=5 -> y´=0
f(x)=xⁿ	f´(x)=n·x^n-1	y=x³ -> y´=3x²
f(x)=e^x	f´(x)=e^x	y=e^x -> y´=e^x
f(x)=ln(x)	f´(x)=1/x	y=3·ln(x) -> y´=3/x
f(x)=sin(x)	f´(x)=cos(x)	y=sin(3x) ->y´=3·cos(3x)
f(x)=cos(x)	f´(x)=-sin(x)	y=cos(5x) ->y´=-5·sin(5x)
f(x)=tan(x)	f´(x)=1/cos²(x)	y=3·tan(x) ->y´=3/cos²(x)

Ableitungsregeln Übersicht

Klickt auf die Ableitungsregel für mehr Informationen, Erklärungen und Beispiele:

Potenzregel

"Exponent vor´s x und dann den Exponenten um eins verkleinern"
Diese Regel müsst ihr fast immer bei einer Ableitung anwenden, wenn keine andere Funktion, wie z.B. Sinus, vorliegt.

Faktorregel

"Der Faktor vor dem x bleibt einfach stehen"
Die Faktorregel ist recht leicht, wenn ein Faktor mit einem Mal vor dem Teil mit der x steht, lasst ihr den einfach stehen und leitet den Teil mit der x ab.

Summen- und Differenzenregel

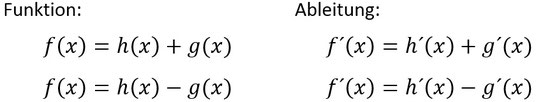
"Jeder Summand wird für sich abgeleitet"
Wenn ihr eine Summe aus einzelnen Summanden mit x-en habt, dann leitet ihr einfach jeden Summanden einzeln ab.

Produktregel

"Erste Funktion abgeleitet mal die zweite, plus die Erste mal die Ableitung der Zweiten"
Diese Regel greift, wenn ihr zwei Funktionen (Teile) mit einem x habt.

Kettenregel

"Die äußere Funktion abgeleitet, mal die Innere abgeleitet"
Die Kettenregel ist von Nöten, wenn eine Funktion in einer anderen Funktion verschachtelt ist.

Quotientenregel

"Wenn zwei Funktionen durcheinander geteilt werden, kommt die Quotientenregel zum Einsatz"
Dies ist die längste Regel, wenn ihr sie vermeiden könnt, dann tut das.

Arbeitsblätter und Spickzettel zur Ableitung

Aufgaben (mit Lösungen) und Spickzettel zu diesem Thema findet ihr über folgenden Button. Dort könnt ihr euch diese kostenlos downloaden.

Arbeitsblätter zur Ableitung

Spickzettel

Was ist die Ableitung und wozu ist sie da?

Die Ableitung ist dafür da, die Steigung einer Funktion an jedem beliebigen Punk anzugeben. Ihr kennt bereits die Berechnung der Steigung durch den Differenzialquotienten, beispielsweise bei den linearen Funktionen (nichts anderes als das Steigungsdreieck), allerdings kann man so ja nur die Steigung an einem Punkt ausrechnen und für Kurven, z.B. Parabeln ist dies erst recht schwer. Deshalb gibt es die Ableitung, sie gibt die Steigung an jedem Punkt der Funktion an, also wenn man ein x einsetzt, erhält man die Steigung an dieser Stelle.

Möchtet ihr nun die Steigung für die Tangente durch den Punkt P an einem x-Wert wissen, schaut ihr bei diesem einfach den y-Wert der Ableitung an, denn das ist die Steigung an diesem Punkt.

Hier seht ihr die Funktion f in grün. In rot wurde die Tangente durch den Punkt P eingezeichnet und ihr bekommt für den Punkt P immer die Steigung angezeigt, wobei ihr diesen Punkt mit dem Schieberegler verschieben könnt. So verändert sich auch die Steigung. Die Steigung wird euch mit dem Punkt M angezeigt, der für jeden x-Wert die passende Steigung der Funktion f als y-Wert hat (z.B. wenn die Funktion die Steigung m=4 am Punkt x=2 hat, dann hat M die Koordinaten (2|4)), wenn ihr dann den Punkt P verschiebt, hinterlässt der Punkt M Spuren, wo er überall war. Lila ist die Ableitung der Funktion f, da wird euch auffallen, dass der Punkt M sich genau auf dieser Linie bewegt, also auf der Ableitung, denn die Ableitung gibt ja, genauso wie der Punkt M, die passende Steigung der Funktion f für einen bestimmten x-Wert an.

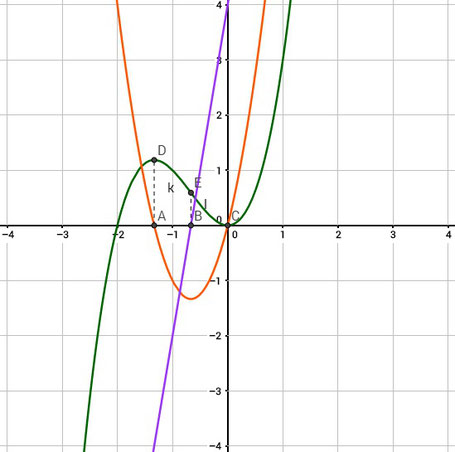
Mehrfache Ableitung und ihre Bedeutungen

Hier seht ihr eine Funktion und ihre Ableitungen in einem Koordinatensystem gezeichnet.

Hier seht ihr die Funktion f in grün und die 1. Ableitung in orange und die 2. Ableitung in lila.

Die Nullstellen der 1. Ableitung sind die Extremstellen der Funktion. Ihr seht die Nullstellen A und C der 1. Ableitung. D und auch C sind dann die Extremstellen der Funktion.
Die Nullstellen der 2. Ableitung sind die Wendepunkte. Ihr seht die Nullstelle der 2. Ableitung B. An der Stelle x ist dann auch die Wendestelle E der Funktion.