Dreieck
Ein Dreieck ist eine Figur, die aus drei Punkten besteht, welche durch Strecken miteinander verbunden sind.
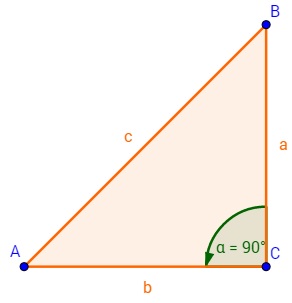
Hier seht ihr das Dreieck ABC. Die Punkte eines Dreiecks werden gegen den Uhrzeigersinn verteilt, also erst A, dann gegen den Uhrzeigersinn B und C. Die Verbindungsstrecken werden dabei nach dem Punkt benannt, welcher gegenüber von ihnen ist, nur mit einem kleinen Buchstaben.
Winkel: Die Winkel werden so benannt, dass bei A immer α ist, bei B β und bei C γ. Das sind die kleinen griechischen Buchstaben für A, B und C.
Fläche eines Dreiecks berechnen
Möchtet ihr die Fläche eines Dreiecks berechnen, müsst ihr erst mal wissen, was die Höhe ist. Diese ist hier rechts (mobil unten) eingezeichnet, es ist die Linie, die von einem Punkt aus senkrecht runter auf gegenüberliegende Seite (dann Grundseite genannt) gezeichnet wird. Die Formel zum Berechnen ist dann:
A = 0,5 · c · h
- A ist die Fläche
- c ist die Grundseite, auf der die Höhe senkrecht steht
- h ist die Höhe
Beispiel zur Berechnung der Fläche
Ihr habt ein Dreieck mit einer Höhe von 3cm und einer Grundseite von 4cm, wie Groß ist die Fläche?
A = 0,5 · 4cm · 3cm = 6cm2
Jetzt wisst ihr, dass das Dreieck eine Fläche von 6cm2 hat.
Beschriftung rechtwinkliges Dreieck
Die Beschriftung im rechtwinkligen Dreieck ist folgende:
- Hypotenuse: Das ist die Seite, die gegenüber vom rechten Winkel liegt
- Ankathete: Das ist die Seite, die am rechten Winkel und am gesuchten Winkel liegt
- Gegenkathete: Das ist die Seite, die gegenüber vom gesuchten Winkel liegt
Höhensatz und Kathetensatz
Mit dem Höhensatz und Kathetensatz kann man Längen in Dreiecken berechnen.
Höhensatz
Kathetensatz
Satz des Pythagoras
Der Satz des Pythagoras ist eine Möglichkeit in rechtwinkligen Dreiecken Längen zu berechnen.
Die Formel vom Satz des Pythagoras ist:
c2=a2+b2
- c ist die Seite, die gegenüber des rechten Winkels liegt
- a ist eine der Seiten, die am rechten Winkel liegt
- b ist die andere Seite, die am rechten Winkel liegt
Arten von Dreiecken
Es gibt viele Arten von Dreiecken. Hier findet ihr eine Übersicht, klickt auf eins und ihr erfahrt alles dazu:
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
