Integrationsregeln in einer Übersicht
Hier eine Übersicht und Erklärung einiger Regeln, die ihr beim Integrieren beachten müsst. Integration einfach erklärt.
Potenzregel
Die Potenzregel wendet man beim aufleiten von Potenzen, dabei wird der Exponent als Kehrbruch vorgezogen und dabei im Nenner und im Exponenten um eins erhöht:
Beispiel:
Faktorregel
Die Faktorregel bei der Integration funktioniert genauso, wie bei der Ableitung, nämlich kann man den Faktor einfach stehen lassen.
Beispiele:
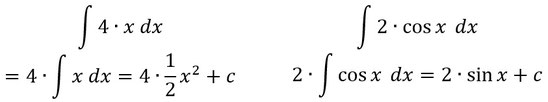
Summenregel
Auch die Summenregel funktioniert genauso, wie bei der Ableitung, ihr könnt also beide Summanden jeweils einzeln integrieren:
Beispiele:
Differenzenregel
Die Differenzenregel funktioniert wie die Summenregel:
Beispiele:
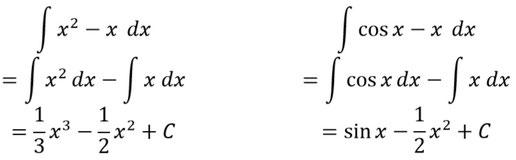
Sonderregel
Wenn ihr einen Bruch habt, wobei der Zähler der abgeleitete Nenner ist, dann ist die Stammfunktion der Logarithmus des Nenners.
Beispiele:
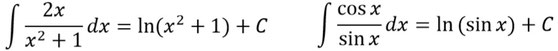
Partielle Integration
Die partielle Integration (oder auch Produktintegration) ist der Produktregel beim Ableiten ähnlich, es ist sozusagen die Umkehrung dieser. Sie ist ein Hilfsmittel, um Funktionen integrieren zu können, bei denen es auf andere Art und Weiße schwer wäre. Hier die allgemeine Formel:
Genauere Erklärung findet ihr in einem extra Kapitel:
Integration durch Substitution
Integration durch Substitution ist die Umkehrung der Kettenregel vom Ableiten. Sie kommt zum Einsatz, wenn eine Funktion „in der anderen drinnen steckt“. Dabei ersetzt man die innere Funktion durch u (kann auch anderer Buchstabe sein), um leichter integrieren zu können. Kann sein, dass ihr eine etwas andere Formel kennt, jedoch finde ich diese deutlich leichter:
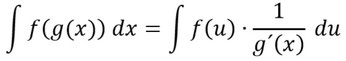
Eine ausführliche Erklärung findet ihr in einem extra Kapitel:
Arbeitsblätter zur Integration
Wenn ihr das Integrieren üben möchtet, könnt ihr das mit unseren kostenlosen Arbeitsblättern machen:
Mehr zur Integration
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
