Kreuzprodukt
Das Kreuzprodukt von zwei Vektoren kommt immer wieder vor. Es wird häufig benötigt um einen Normalenvektor zu bestimmen, also einen Vektor, der senkrecht zu den anderen Vektoren steht. Das Ergebnis ist nämlich ein Vektor, der senkrecht zu den beiden Vektoren mit denen er berechnet wurde, steht. Berechnet wird dies so:

Da ihr wahrscheinlich die Formelsammlung benutzen dürft, müsst ihr euch diese Formel fürs Abi meist nicht merken (selbst im Mathestudium merkt die sich kaum einer ;)).
Beispiel zum Berechnen des Kreuzprodukts
Hier ein Beispiel, wie ihr das Kreuzprodukt berechnen könnt.
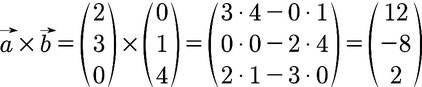
Normalenvektor
Mit dem Kreuzprodukt könnt ihr recht leicht den Normalenvektor bestimmen, indem ihr einfach die zwei Vektoren, zu denen der Normalenvektor senkrecht stehen soll, mit dem Kreuzprodukt wie oben berechnet. So erhaltet ihr den Normalenvektor, beispielsweise für Ebenen oder Ähnliches.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.



