Geometrische Figuren
In der Geometrie kommen verschiedene Arten von Figuren vor, diese stellen wir euch hier vor. Klickt auf das, was ihr sucht und ihr scrollt direkt zur richtigen Stelle:
Übersicht
Punkt
Ein Punkt ist das, was ihr auch im Alltag darunter versteht. Einfach nur ein Punkt. Dieser kann dann in einem Koordinatensystem an einer bestimmten Stelle vorkommen, die "Adresse" des Punktes nennt man dann Koordinaten, die sagen euch, wo der Punkt in einem Koordinatensystem liegt. Geschrieben werden die Koordinaten, indem man davor den "Namen" des Punktes als Großbuchstaben schreibt, und danach in Klammern erst die x-Koordinate und danach die y-Koordinate, also so:
P(x|y)
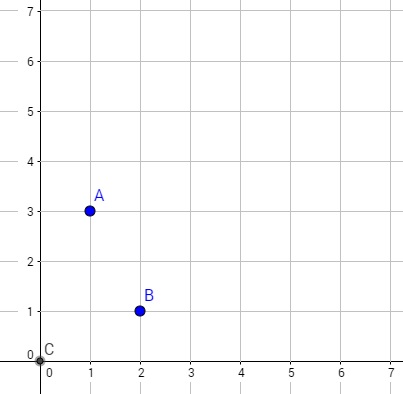
Hier seht ihr 3 Punkte, A, B und C. Die Koordinaten der Punkte sind:
- A(1|3)
- B(2|1)
- (1|3)
- C(0|0) (C ist ein besonderer Punkt, nämlich der Koordinatenursprung, also da, wo sich die x- und y-Achse schneiden und beide Koordinaten 0 sind.)
Mehr zu Punkten: Abstand Punkt und Punkt
Gerade
Eine Gerade ist eine unbegrenzte, unendlich lange Linie. Diese Linie besteht aus unendlich vielen Punkten. Dies ist vielleicht schwer vorzustellen, aber ihr müsst nur wissen, dass sie immer gerade ist (deshalb heißt sie auch so) und immer weiter in beide Richtungen geht.

Hier seht ihr eine Gerade, die g heißt und durch die Punkte B und C verläuft.
Halbgerade
Eine Halbgerade ist ähnlich wie eine Gerade, nur dass sie in eine Richtung nicht unendlich lang weiter geht, sondern an einem Punkt endet.

Hier seht ihr eine Halbgerade, sie hat einen Anfangspunkt bei A, aber keinen Endpunkt, verläuft aber durch B.
Strecke
Die Strecke ist wie eine Halbgerade, nur dass sie nicht nur auf einer Seite einen Endpunkt hat, sondern an beiden Seiten.

Hier seht ihr eine Strecke, sie hat einen Anfangspunkt A und einen Endpunkt B. Die Strecke hat in diesem Beispiel den Namen f.
Dreieck
Ein Dreieck ist eine Figur, die aus drei Punkten besteht, welche durch Strecken miteinander verbunden sind.

Hier seht ihr ein Dreieck, welches aus den Punkten A, B und C besteht.
Benennung: Die Punkte eines Dreiecks werden meist gegen den Uhrzeigersinn verteilt, also erst A, dann gegen den Uhrzeigersinn B und C. Die Verbindungsstrecken werden dabei nach dem Punkt benannt, welcher gegenüber von ihnen ist, nur mit einem kleinen Buchstaben.
Winkel: Die Winkel werden so benannt, das bei A immer α ist, bei B β und bei C γ. Das sind die griechischen Buchstaben für A, B und C.
Ungleichmäßiges Dreieck
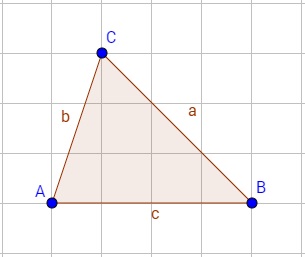
Bei einem ungleichmäßigen Dreieck sind alle Seiten unterschiedlich lang und alle Winkel sind unterschiedlich.
Gleichschenkliges Dreieck
Gleichseitiges Dreieck
Spitzwinkliges Dreieck

Bei einem spitzwinkligen Dreieck sind alle 3 Winkel kleiner als 90°.
Rechtwinkliges Dreieck

Bei einem rechtwinkligen Dreieck ist ein Winkel genau 90° groß.
Stumpfwinkliges Dreieck

Ein stumpfwinkliges Dreieck hat einen Winkel der größer als 90° ist.
Viereck
Ein Viereck ist ähnlich wie ein Dreieck, nur dass es anstatt aus drei, aus vier Punkten besteht, welche mit Verbindungsstrecken verbunden werden.

Hier seht ihr ein Viereck, welches aus den Punkten A, B, C und D besteht.
Benennung: Die Ecken eines Vierecks werden meist gegen den Uhrzeigersinn benannt, also erst A und dann gegen den Uhrzeigersinn weiter B, C und D.
Die Verbindungsstrecken werden, wie bei Dreiecken, mit kleinen Buchstaben benannt, dabei heißt die Strecke zwischen A und B a, die zwischen B und C b, zwischen C und D c und die Strecke zwischen D und A d.
Winkel: Die Winkel werden so benannt, dass der Winkel bei A α heißt, bei B β, bei C γ und bei D δ. Das sind die griechischen Buchstaben für A, B, C und D.
Allerdings gibt es viele Arten von Vierecken, die unterschiedlich benannt werden:
Quadrat

Das Quadrat ist ein Viereck, bei welchem alle vier Seiten gleich lang sind und dazu parallel, also es hat 4 rechte Winkel.
Rechteck

Ein Rechteck ist ein Viereck, dessen Seiten alle parallel sind und es daher 4 rechte Winkel hat. Eine spezielle Form des Rechtecks ist das Quadrat.
Trapez
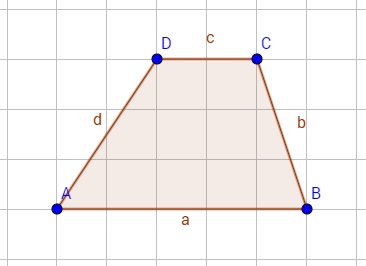
Ein Trapez ist ein Viereck, welches zwei parallele Seiten hat, hier im Beispiel a und c. Das Rechteck ist also auch ein spezielles Trapez.
Gleichschenkliges Trapez

Ein gleichschenkliges Trapez hat zwei parallele Seiten (hier a und c) und zusätzlich sind beide Schenkel (die nicht parallelen Seiten, hier b und d) gleich lang.
Rechtwinkliges Trapez

Ein rechtwinkliges Trapez besitzt zwei parallele Seiten und eine der beiden Schenkel ist senkrecht zu den parallelen Seiten. Hier ist d senkrecht zu den parallelen Seiten c und a.
Parallelogramm

Ein Parallelogramm ist ein Viereck, welches zwei Paare an parallelen Seiten hat, hier zum Beispiel sind a und c parallel und d und b.
Raute

Eine Raute hat vier gleich lange Seiten, also ist das Quadrat eine besondere Raute.
Drachenviereck

Ein Drachenviereck ist ein Viereck, welches eine diagonale Symmetrieachse besitzt (hier gestrichelt eingezeichnet). Das bedeutet, man kann das Viereck an dieser Symmetrieachse spiegeln und es kommt wieder dasselbe raus.
Kreis

Ein Kreis hat keine Ecken, besitzt dafür einen Mittelpunkt, Radius und Durchmesser. Der Radius ist der Abstand von außen bis zum Mittelpunkt. Der Durchmesser ist die Breite des Kreises und ist einfach der doppelte Radius.