Funktionen verschieben
Man kann Funktionen modulieren, also zum Beispiel in x- und y-Richtung verschieben. Hier erklären wir euch genau, wie das geht und wie ihr erkennt, ob eine Funktion verschoben wurde.
Funktion in y-Richtung verschieben
Ihr könnt Funktionen in y-Richtung verschieben, indem ihr an die Funktion eine Zahl addiert (nach oben verschieben) oder subtrahiert (nach unten verschieben). Also sieht eine Verschiebung um a dann so aus:
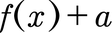
- Ist a positiv, ist es eine Verschiebung nach oben
- Ist a negativ, ist es eine Verschiebung nach unten
Beispiele für Verschiebung in y-Richtung
Hier einige Beispiele von Funktionen, die in y-Richtung verschoben wurden. Rot ist die verschobene Funktion und grün die Ursprüngliche.
Funktion:
Funktion um 1 nach oben Verschoben:
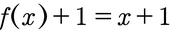
Hier seht ihr wie die Funktion y=x um 1 nach oben verschoben wurde. Möchtet ihr eine Funktion nach oben verschieben, müsst einfach den Wert, um den ihr nach oben oder unten verschieben wollt, daran addieren oder subtrahieren.
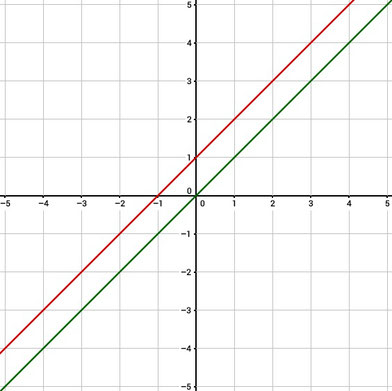
Funktion:
Funktion um 2 nach unten verschoben:
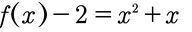
Diese Funktion wurde um 2 nach unten verschoben, dazu wird hinten an die Funktion 2 subtrahiert.
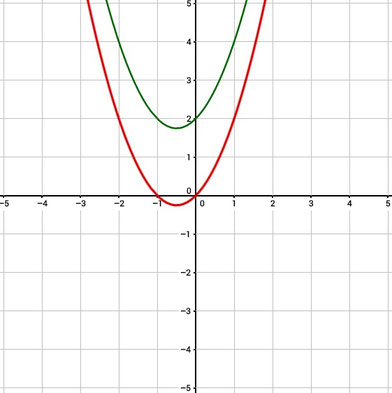
Funktion:
Funktion um 2 nach oben verschoben:
Diese Funktion wurde um 2 nach oben verschoben.
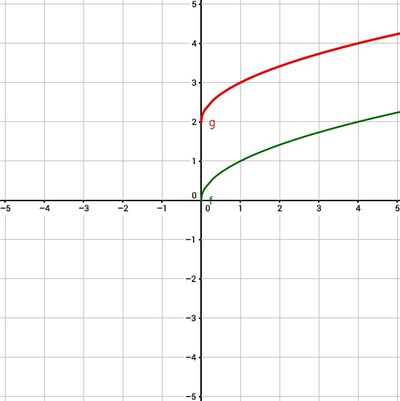
Funktion in x-Richtung verschieben
Um eine Funktion in x-Richtung zu verschieben (also nach links oder rechts) müsst ihr eine Zahl direkt an das x in der Funktion addieren bzw. subtrahieren. Das sieht dann so aus:
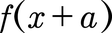
- Ist a negativ ist es eine Verschiebung nach rechts
- Ist a positiv ist es eine Verschiebung nach links
Beispiele für Verschiebung in x-Richtung
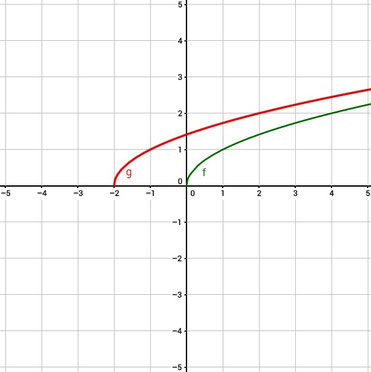
Folgende Beispiele zeigen Funktionen, die in x-Richtung verschoben wurden. Rot ist dabei die verschobene Funktion und grün die Ursprüngliche.
Funktion:
Funktion um 2 nach links verschoben:
Diese Funktion wurde um 2 nach links verschoben. Wie ihr seht, schreibt man, wenn man die Funktion verschiebt, den Wert, um den sie verschoben wird, direkt an das x.
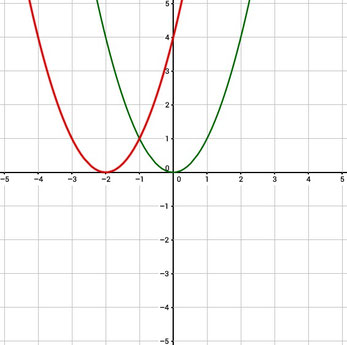
Funktion:
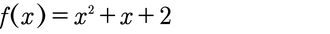
Funktion um 2 nach rechts verschoben:
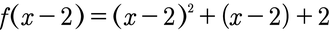
Hier seht ihr eine Funktion, die um 2 nach rechts verschoben wurde. Wie ihr seht, wird dabei an JEDES x die Verschiebung direkt hinten dran geschrieben!
Funktion:
Funktion um 2 nach links verschoben:
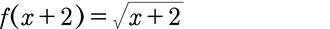
Diese Funktion wurde um 2 nach links verschoben, wie ihr seht. Wieder die Verschiebung direkt an das x mit unter die Wurzel schreiben!
Verschiebungen von Funktionen erkennen
Um eine Verschiebung einer Funktion zu erkennen, müsst ihr darauf achten, ob eine Zahl hinten an der Funktion addiert oder subtrahiert wird, dann ist sie nach oben oder unten verschoben. Ist jedoch eine Zahl direkt am x addiert oder subtrahiert, also zum Beispiel mit unter der Wurzel oder unter einem Exponenten, dann ist die Funktion nach links oder rechts verschoben.
Beispiele:
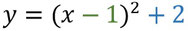
Diese Funktion wurde im Vergleich zur Funktion y=x2 um 1 nach rechts und 2 nach oben verschoben.
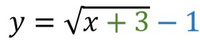
Diese Funktion wurde im Vergleich zur Funktion 𝑦 = √x um 3 nach links und 1 nach unten verschoben.
Aufgaben zum Verschieben von Funktionen
Hier könnt ihr das Verschieben von Funktionen üben. Um die Lösung zu sehen klickt auf "Einblenden".
| Um was wurde die Funktion f(x)=x verschoben: f(x)=x-1? | Einblenden | |
| Um was wurde die Funktion f(x)=x2 verschoben: f(x)=(x+2)2+1? | Einblenden | |
| Um was wurde die Funktion f(x)=x2 verschoben: f(x)=(x-2)2-1? | Einblenden | |
| Um was wurde die Funktion f(x)=x6 verschoben: f(x)=(x+5)6+5? | Einblenden | |
Arbeitsblätter und Spickzettel zum Verschieben von Funktionen
Weitere Aufgaben und Spickzettel zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Übungsblätter downloaden. Lösungen zu den Aufgaben findet ihr dort ebenfalls:
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
