Varianz und Standardabweichung
Varianz
Die Varianz ist der Durchschnittliche quadratische Abstand eurer Werte. Dieser Wert sagt aus, wie stark die Wahrscheinlichkeitsverteilung der Werte streut, allerdings lassen sich mit der Varianz selbst keine konkreten Aussagen treffen, allerdings benötigt man sie zum Berechnen der Standardabweichung (hier weiter unten), weshalb sie wichtig ist. Was die Varianz konkret ist, ist daher für euch nicht wichtig, ihr braucht sie nur für die Standardabweichung, einen anderen Zweck erfüllt sie nicht. Berechnet wird sie ähnlich wie der Erwartungswert. Die Formel sieht so aus:
- x sind die Werte die rauskommen können
-
- Beim Würfeln also die Augenzahlen
- Beim Lotto, das Geld, welches ihr gewinnen könnt
- p sind die dazugehörigen Wahrscheinlichkeiten
-
- Beim Würfeln also zum Beispiel die Wahrscheinlichkeit eine 1 zu würfeln
- Beim Lotto die Wahrscheinlichkeit eine bestimme Geldsumme zu gewinnen
- μ ist der Erwartungswert, diese ist in der Formel immer derselbe, also müsst ihr ihn nur einmal berechnen und dann in die Formel einsetzen.
Beispiel zur Berechnung der Varianz
Ihr möchtet die Varianz der Augenzahl berechnen, wenn ihr mit 2 Würfeln würfelt, dass macht ihr dann so:
- Berechnet den Erwartungswert. Wie das geht, findet ihr im Artikel zum Erwartungswert. (der Erwartungswert ist 7)
- Setzt alles in die Formel ein:
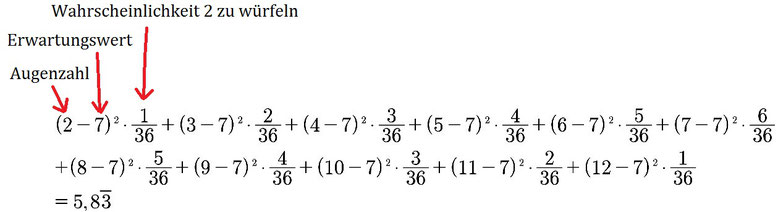
5,83 ist dann eure Varianz.
Aufgabe: Varianz berechnen
Klickt auf Einblenden, um die Lösung der Aufgabe zu sehen.
| Ihr wirft einen Würfel, der Erwartungswert liegt bei 3,5. Wie groß ist die Varianz. | Einblenden | |
Standardabweichung
Die Standardabweichung ist die Streuung um den Mittelwert, dies gibt also an, wie groß der Erwartungswert abweichen kann. Ist beispielsweise die Standardabweichung bei einem Glücksspiel groß, bedeutet es, wenn ihr paar Mal spielt, kann es gut sein, dass ihr deutlich mehr Verlust macht als der Erwartungswert "vorhersagt", aber genauso deutlich mehr Gewinn. Also geht die Standardabweichung immer in beide Richtungen vom Erwartungswert. Es ist also die Größe, die er abweichen kann. Berechnet wird die Standardabweichung so:
Beispiel zur Berechnung der Standardabweichung
Die Standardabweichung der Augenzahl, wenn man mit 2 Würfeln würfelt, berechnet ihr so:
- Berechnet die Varianz, wie das geht, seht ihr oben.
- Zieht die Wurzel der Varianz
Dann erhaltet ihr den Wert 2,41 als Standardabweichung. Das ist die mittlere Abweichung um den Mittelwert 7, wenn man mit 2 Würfeln würfelt. Den Wert kann man mit dem Erwartungswert dann so angeben:
7 ±2,41
Das bedeutet, man würfelt im Durchschnitt eine 7, aber es kann auch 2,4 mehr oder weniger sein, da der Wert um so viel abweichen kann.
Aufgabe: Standardabweichung berechnen
Klickt auf Einblenden, um die Lösung der Aufgabe zu sehen.
| Ihr wirft einen Würfel, der Erwartungswert liegt bei 3,5 und die Varianz bei 2,92. Wie groß ist die Standartabweichung? | Einblenden | |
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
