Integration durch Substitution
Integration durch Substitution ist die Umkehrung der Kettenregel (beim Ableiten). Sie kommt zum Einsatz, wenn eine Funktion „in der anderen drinnen steckt“. Dabei ersetzt man die innere Funktion durch u (kann auch anderer Buchstabe sein), um leichter integrieren zu können. Die innere Funktion wird dabei separat berechnet. Hier die Formel zur Integration durch Substitution. Hinweis: Es kann sein, dass ihr eine etwas andere Formel kennt, jedoch finden wir diese deutlich leichter:

Integration durch Substitution berechnen
- Sucht euch den Teil der Funktion, den ihr substituieren wollt.
- Tipp: Immer den Teil ersetzen, der selbst in einer Funktion steckt.
- Z.B. bei y=cos(3x+1) würdet ihr 3x+1 ersetzen.
- Ersetzt die Innere Funktion durch das u.
- Leitet die Funktion, die ihr ersetzt habt, ab und schreibt sie als Kehrbruch mit einem Mal an die Funktion.
- Jetzt müsst ihr nach u Integrieren
- Setzt in das Ergebnis das, was ihr durch u ersetzt habt, wieder für u ein.
Beispiel zur Integration durch Substitution
Bei dieser Funktion müsst ihr die Integration durch Substitution durchführen, da eine Funktion in der Anderen „drinnen steckt“.
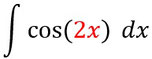
- Stellt fest, welchen Teil ihr durch u ersetzen müsst, also die innere Funktion.
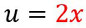
- Leitet diese Funktion jetzt ab (die innere Funktion, die ihr ersetzt).
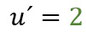
- Setzt nun alles so wie in der Formel ein, also ersetzt die innere Funktion durch u und multipliziert daran den Kehrbruch der Ableitung der inneren Funktion.

- Integriert nun nach u (aufpassen nicht nach x!). Leitet also so ab, als wäre u das x.
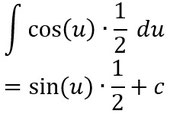
- Jetzt ersetzt ihr nur noch das u durch die innere Funktion (also 2x) und ihr seid fertig.
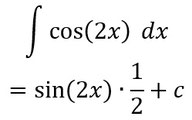
2. Beispiel: Integration durch Substitution berechnen
Bestimmt die innere Funktion, die ihr ersetzen müsst. Hier ist es der Exponent vom e, also -3x2.

- Also ist das u:
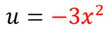
- Leitet das u ab:

- Jetzt setzt ihr dies in die Formel von ganz oben ein. Also ersetzt die innere Funktion durch u und multipliziert daran den Kehrbruch der von euch berechneten Ableitung der inneren Funktion.

- Kürzt wenn möglich.

- Jetzt integriert ihr nach u. Da die e-Funktion gleich bleibt, ist das hier nicht so schwer.
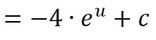
- Setzt jetzt nur noch die innere Funktion für u ein und ihr seid fertig.
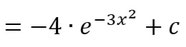
Erkennen der inneren Funktion
Die innere Funktion ist immer die, die in einer anderen Funktion „drinnen steckt“. Ein Merkmal der inneren Funktion ist, dass wenn man sie in die Funktion durch ein x ersetzen würde, die Funktion einfach zu integrieren wäre.
Meistens ist die innere Funktion das, was …
- … im Cosinus, Sinus oder Tangens steht.
- f(x) = cos(2x+1) -> u=2x+1
- … im Exponenten der e-Funktion steht.
- f(x) = e4x+1 -> u=4x+1
- … im Nenner eines Bruchs steht
- f(x) = 1/(x2+3) -> u=x2+3
- … im Logarithmus steht
- f(x) = ln(x2) -> u=x2
Aufgaben zur Integration durch Substitution
Wenn ihr üben möchtet, findet ihr Aufgaben mit Lösung auch auf unserer Seite. Guckt einfach hier:
