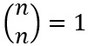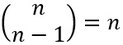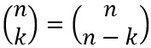Binomialkoeffizient - Formel und Berechnung
Der Binomialkoeffizient ist eine Funktion, mit welcher sich Aufgaben der Kombinatorik lösen lassen. So kann man damit beispielsweise berechnen, wie viele Möglichkeiten es gibt k Objekte aus n Objekten zu wählen (ohne zurücklegen, ohne Betrachtung der Reihenfolge). Zum Beispiel, wie viele Möglichkeiten es beim Lotto 6 aus 49 gibt. So sieht der Binomialkoeffizient aus:
Die Ausrufezeichen bedeuten Fakultät.
Beispiel zur Berechnung des Binomialkoeffizienten
Es werden 4 aus 6 Kugeln gezogen. Dabei wird nicht zurückgelegt und die Reihenfolge, mit der die Kugeln gezogen werden, ist egal.
Lösung zur Berechnung:
Setzt für n=6 ein und für k=4. Denn für n wird immer die gesamte Anzahl eingesetzt und für k die Anzahl, welche davon ausgesucht wird. Dann ergibt sich als Lösung, dass es 15 Möglichkeiten gibt, 4 aus 6 Kugeln zu ziehen.
2. Beispiel: Binomialkoeffizient berechnen
In einer Klasse mit 30 Schülern sollen 3 Schüler abgefragt werden. Der Lehrer zieht die Namen zufällig aus einem Hut, in dem Zettel mit den Namen der Schüler sind. Wie viele mögliche Kombinationen von abgefragten Schülern gibt es?
Lösung:
Ihr setzt für n=30 ein und für k=3. Dann erhaltet ihr die Lösung, nämlich das es 4060 Möglichkeiten gibt.
Rechenregeln
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
