Simplex Algorithmus
Der Simplex-Algorithmus, oder auch Simplexverfahren genannt, ist eine Möglichkeit lineare Ungleichungen zu lösen und dessen Maximum anzugeben.
Meist habt ihr dann eine Zielfunktion und Bedingungen wie folgt gegeben:
- Zielfunktion:
- z=c1x1+c2x2+c3x3+d
- Bedingungen:
- a11x1 + a12x2 + a13x3 ≤ b1
- a21x1 + a22x2 + a23x3 ≤ b2
- a31x1 + a32x2 + a33x3 ≤ b3
Achtung: Wichtig ist, dass das es immer kleiner-gleich b ist und nie größer-gleich b!! Wenn nicht muss umgeformt werden. (Siehe Beispiel unten)
Mit diesen Werten erhält man dann diese Tabelle:
Simplexverfahren Schritt für Schritt
Habt ihr nun alle Angaben und ihr sollt das Maximum des Ungleichungssystems bestimmen, dann geht ihr so vor (Beschriftung wird aus der Tabelle darüber verwendet, ihr könntet andere Buchstaben haben):
- Tragt alles in die Tabelle ein
- Jetzt muss das Pivot-Element bestimmt werden. Das geht so: Schaut, ob bei RS (rechte Seite/Spalte) mindestens einer der Werte (b) negativ ist.
- Wenn alle positiv sind, dann guckt ihr, welches das kleinste negative c in der unteren Zeile ist. Dort ist dann eure Pivot-Spalte. Um nun das Pivot-Element zu bestimmen, teilt ihr das jeweilige b durch die Zahl der Pivot-Spalte, welches in derselben Zeile ist (b:a). In der Zeile, wo der kleinste Wert rauskommt, ist das Pivot-Element. (Beispiel Schritt 4)
- Wenn eines oder mehrere Werte b negativ sind, wählt ihr das kleinste negative Element aus (falls nur eines da ist, dann halt dieses). In der Zeile, in der diese Zahl ist, ist die Pivot-Zeile. Das Pivot-Element ist dann die negative Zahl in der Pivot-Zeile. (Sollte es mehrere negative Zahlen in der Pivot-Zeile geben, könnt ihr euch selbst für eines entscheiden.) (Beispiel Schritt 2)
- Habt ihr das Pivot-Element, müsst ihr alle Elemente in der Pivot-Spalte auf 0 bringen, außer das Pivot-Element selber. (Beispiel Schritt 3)
- Jetzt beginnt ihr wieder von Anfang, bis kein b und kein c mehr negativ ist. Dann seid ihr fertig. Das d ist dann das Maximum. (Beispiel Schritt 7)
Beispiel
Man hat gegeben:
- Zielfunktion:
- z=2x1+x2
- Bedingungen:
- x1+x2 ≥ 3 -> -x1-x2 ≤ 3
- 3x1 ≤ 2x2+9 -> 3x1-2x2 ≤ 9
- x2 ≤ 6
- x1 und x2 ≥ 0
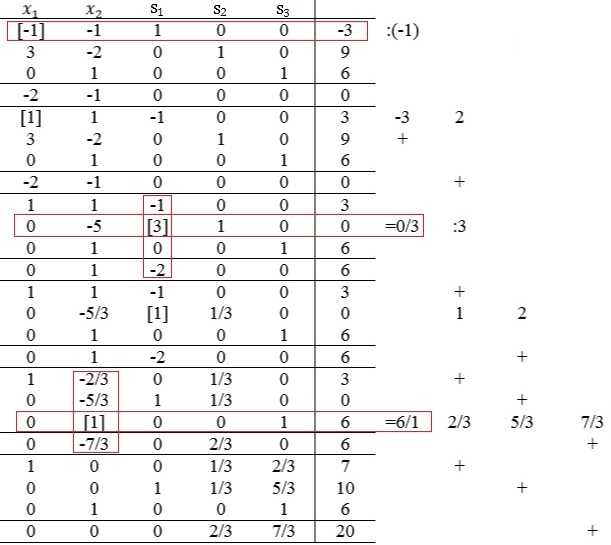
Schritt 1: Tabelle
Wenn ihr alles richtig umgeformt habt, tragt alles in eure Tabelle ein. (Siehe Schritt 2)
Schritt 2: Pivot Element bestimmen
- Geht wie oben beschrieben vor. Da hier eine negative Zahl in der rechten Spalte ist, ist dort die Pivot-Zeile (wären dort mehrere negative Zahlen, dann muss man die Kleinste negative nehmen).
- Das Pivot-Element [-1] ist dann die negative Zahl in der Pivot-Spalte. Hier gibt es 2 Stück, dann könnt ihr euch frei für ein Pivot-Element entscheiden.
Schritt 3: Umformen
- Jetzt formt ihr so um, dass bis auf das Pivot-Element alle Zahlen in der Pivot-Spalte 0 sind. Dazu nehmt ihr eine Zeile mal eine Zahl und dann plus oder minus eine andere Zeile, sodass das jeweilige Element in der Pivot-Spalte 0 wird.
- Hier wurde z.B. die Pivot-Zeile mal -3 genommen und dann plus die 2. Zeile. So wird aus der 3 in der Pivot-Spalte eine 0.
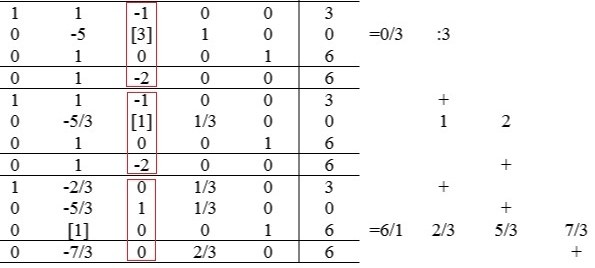
Schritt 4: Nächstes Pivot-Element bestimmen
- Wie ihr seht, ist in der untersten Spalte immer noch ein negatives Element, deshalb seid ihr noch nicht fertig.
- Bestimmt das nächste Pivot-Element. Da in der rechten Spalte alle Elemente positiv sind, guckt ihr euch die in der untersten Zeile an. Das kleinste negative Element (hier -2) gibt die Pivot-Spalte vor.
- Dann teilt ihr die Zahlen der letzten Spalte durch die jeweiligen Zahlen der Pivot-Spalte. Das kleinste positive Ergebnis gibt die Pivot-Zeile und so auch das Pivot-Element an. Die Ergebnisse sind hier:
-
- 1. Zeile: 3/-1=-3. Das Ergebnis ist negativ, wird also nicht beachtet.
- 2. Zeile: 0/3=0 Ist das kleinste Ergebnis, also dort ist die Pivot-Zeile.
- 3. Zeile: 6/0 geht nicht! Man darf nicht durch 0 teilen, also wird das Ergebnis auch nicht berücksichtigt.
Schritt 5: Umformen
- Jetzt formt ihr so um, dass bis auf das Pivot-Element alle Zahlen in der Pivot-Spalte 0 sind.
Schritt 6: Nächstes Pivot Element bestimmen
- Immer noch gibt es eine negative Zahl in der letzten Spalte, daher das Ganze noch einmal.
- Also Pivot-Spalte bestimmen, durch kleinste negative Zahl, dann Zahlen der rechten Spalte durch die jeweiligen Zahlen der Pivot-Spalte teilen, kleinstes positives Ergebnis gibt die Pivot-Zeile an.
Schritt 7: Umformen und Ergebnis
- Das Ergebnis habt ihr dann, wenn alle Zahlen in der unteren Zeile und rechten Spalte positiv sind.
- Das Ergebnis ist dann ganz unten rechts, hier 20.
- x1 ist dann 7 (könnt ihr ablesen, indem ihr in der Zeile, in der bei der x1-Spalte die 1 steht, guckt welche Zahl dort in der rechten Spalte steht.)
- x2 ist dann 6 (könnt ihr genauso wie x1 bestimmen.)
- Ihr könnt auch noch überprüfen, ob ihr richtig gerechnet habt, indem ihr x1 und x2 in die Zielfunktion einsetzt und guckt, ob das selbe rauskommt, wie unten rechts im Eck:
- z=2x1+2x2 = 2·7+6 = 20 ✓