Verbindungsvektor berechnen
Möchtet ihr den Verbindungsvektor zweier Punkte wissen, müsst ihr dazu nur die Koordinaten (bzw die Vektoren der Punkte) voneinander Abziehen mit der Regel "Spitze minus Fuß". Das bedeutet, ihr zieht den Punkt, an dem der Vektor beginnen soll, von dem Punkt ab, an dem der Vektor enden soll. Das sieht wie folgt aus:

Der Vektor hier darunter ist vom Koordinatenursprung bis zum Punkt A. Man schreibt ihn so, da er vom Ursprung (im englischen Origin, deshalb O), bis zum Punkt A geht. Es sind einfach die Koordinaten dieses Punktes.
Hier seht ihr den Verbindungsvektor u zwischen A und B.
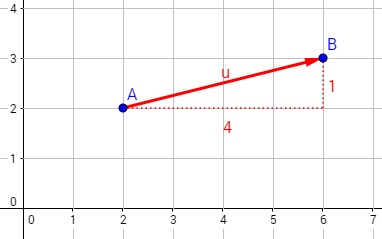
Beispiel 2D
Wenn ihr den Verbindungsvektor zwischen diesen beiden Punkten berechnen möchtet....

...rechnet ihr es wie oben beschreiben aus, also dort, wohin der Vektor zeigen soll, minus dort wo er beginnen soll:

Das Ergebnis sieht dann so aus (wir haben den Vektor dann einfach u genannt, muss man aber nicht):

Beispiel 3D
Habt ihr nun zwei Punkte A und B und wollt den Vektor von A(1|3|2) nach B(4|2|3) wissen, dann macht ihr das so:

Das Ergebnis ist der Verbindungsvektor von A nach B.
Hier könnt ihr euch den Vektor mal in 3D angucken:
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.



