Gebrochenrationale Funktionen
Übersicht:
Allgemeines zu gebrochenrationalen Funktionen
Eine gebrochenrationale Funktion ist eine Funktion, welche aus dem Quotienten zweier Polynome besteht, also aus zwei Funktionen der Form g(x)=a1xn+...+anx0 also zum Beispiel: x3+3x2+5x. Wenn g(x) und h(x) Polynome sind, sieht eine gebrochenrationale Funktion so aus:
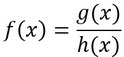
Beispiel:

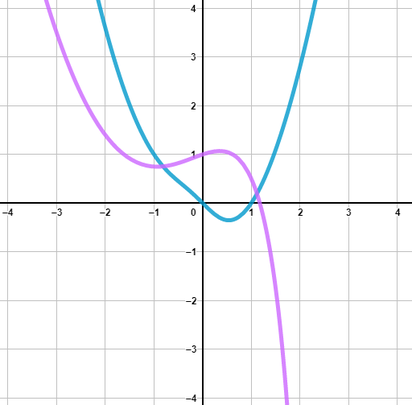
Hier seht ihr diese beiden Funktionen gezeichnet:
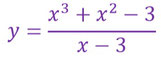

Zähler- und Nennergrad
Mit Zähler- und Nennergrad ist der Grad des Polynoms im Zähler und Nenner gemeint. Dieser ist die höchste Potenz im Zähler bzw. Nenner. Schaut was der höchste Exponent im Nenner bzw. Zähler ist, dies ist dann der Grad des Nenners bzw. Zählers.
Beispiele:

Der Zählergrad ist 3 und der Nennergrad ist 1.

Der Zählergrad hier ist 4 und der Nennergrad ist 2.
Arten von Gebrochenrationalen Funktionen
- Ist der Zählergrad größer als der Nennergrad, nennt man die Funktion unecht gebrochenrationale Funktion
- Ist der Nennergrad größer als der Zählergrad, nennt man die Funktion echt gebrochenrationale Funktion.
Asymptoten
Wie ihr die Asymptoten von gebrochenrationalen Funktionen berechnen könnt, findet ihr in einem separaten Artikel:
Definitionslücke
An den Stellen an der der Nenner 0 ist, ist eine Definitionslücke:
- Dort kann eine hebbare Definitionslücke vorliegen, also eine Definitionslücke, die wegfällt, wenn man den Bruch kürzt, dies kann unter anderem der Fall sein, wenn Nennergrad=Zählergrad.
- Wenn sie durch kürzen nicht wegfällt, gibt es an der Stelle eine Definitionslücke, dort ist dann eine Asymptote parallel zur y-Achse, an die sich der Graph immer weiter annähert, welche er aber nie berührt. Das nennt man dann Polstelle.
Nullstellen gebrochenrationaler Funktionen
Nullstellen einer gebrochenrationalen Funktion sind an den Nullstellen des Zählers, das bedeutet, ihr könnt den Nenner einfach nicht beachten und die Nullstellen des Zählers wie gewohnt berechnen, im Artikel zu Nullstellen wird noch mal erklärt wie.
Beispiel:

Es ist die Nullstelle dieser Funktion gesucht.


