Stammfunktion berechnen
Die Stammfunktion ist die Funktion, die man beim Integrieren (Aufleiten) einer Funktion erhält. Leitet man die Stammfunktion wiederum ab, dann erhält man wieder die ursprüngliche Funktion. Daher ist das Integrieren (Aufleiten) das Gegenteil der Ableitung. Hier eine einfache Erklärung zum Thema.
Bilden der Stammfunktion
Hier findet ihr die Stammfunktionen F(x) für alle Arten von Funktionen. Integrieren ist das Gegenteil vom Ableiten, man überlegt also: Was müsste man ableiten, um diese Funktion f(x) zu erhalten? Vergesst deshalb nicht das +c (Konstante) hinter die Stammfunktion zu schreiben! Leitet man nämlich die Stammfunktion ab, fällt dieses +c wieder weg (Ableitungsregel), weshalb man beim Aufleiten nicht weiß, welche (und ob) dort (F(x)) eine Konstante steht.
Allgemeine Schreibweise
Allgemein wird die Stammfunktion so dargestellt:
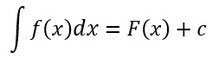
Konstante Funktion
Die Stammfunktion einer konstanten Funktion ist die Konstante mal x (und das c nicht vergessen!).
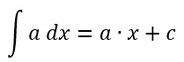
Beispiele:
Potenzfunktion
Bei der Potenzfunktion erhält man die Stammfunktion, indem man den Exponenten um eins erhöht und dann auch als Kehrbruch vor das x schreibt:
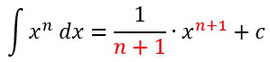
Beispiele:
e-Funktion
Da bei der Ableitung die e-Funktion immer gleich bleibt, ist es bei der Aufleitung genauso:
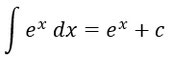
Logarithmusfunktion
Die Stammfunktion für die Logarithmusfunktion sieht wie folgt aus:
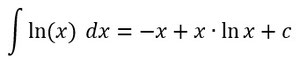
Bruchfunktion
Hat man einen Bruch, mit x im Nenner, dann erhält man den Logarithmus als Stammfunktion (denn wenn man die Logarithmusfunktion ableitet, erhält man einen Bruch mit x im Nenner). Aber aufpassen, in den Logarithmus darf man nur positive Werte für x einsetzen, deshalb die Betragsstriche.
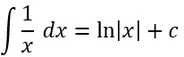
Sinusfunktion
Die Stammfunktion der Sinusfunktion ist die negative Cosinusfunktion.
Cosinusfunktion
Die Stammfunktion der Cosinusfunktion ist die Sinusfunktion:
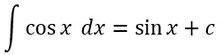
Tangensfunktion
Die Stammfunktion des Tangens leitet sich aus seiner Definition ab:
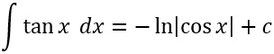
Integralrechenregeln
Um richtig Aufleiten zu können und Stammfunktionen zu bestimmen, müsst ihr die Rechenregeln für Integrale kennen. Diese findet ihr hier:
Beispiele zu den Integrationsregeln
Um die Stammfunktion von f(x)=x2 (und anderen Potenzfunktionen) zu bestimmen, geht ihr so vor:
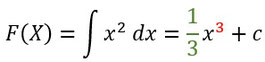
- Erhöht den Exponenten um 1.
- Schreibt den Kehrbruch dieses "neuen" Exponenten als Faktor vor das x, also 1 durch den um 1 erhöhten Exponenten.
- Fertig das ist die "Aufleitung".
Hier seht ihr, wie die Stammfunktion von f(x)=x berechnet wurde:
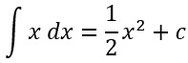
- Exponent um 1 erhöhen
- "Neuen" Exponenten als Kehrbruch vor das x schreiben
Hier wurde die Stammfunktion von f(x)=4x berechnet:
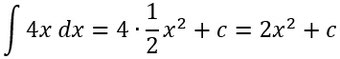
- Exponenten um 1 Erhöhen
- "Neuen" Exponenten als Kehrbruch vor das x schreiben
- Nur noch das, was vor dem x steht verrechnen
Das berechnen von längeren Stammfunktionen geht genauso. Dabei gilt die Produktregel genauso, wie bei der Ableitung:
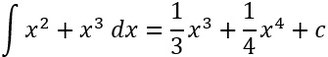
- Beide Exponenten jeweils um 1 erhöhen
- Den jeweils "neuen" Exponenten vor das jeweilige x schreiben
Aufgaben zur Stammfunktion
Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Arbeitsblätter downloaden. Lösungen zu den Aufgaben findet ihr dort ebenfalls:
Mehr zu Integralen und Co.
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
