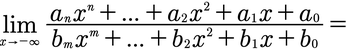Grenzwerte von Funktionen berechnen
Hier wird das Bestimmen und Berechnen der Grenzwerte von Funktionen einfach erklärt. Hier Übersicht der Seite (klickt auf ein Thema um direkt dort hin zu scrollen):
Der Limes
Mit dem Limes können Grenzwerte angegeben werden. Der Limes beschreibt, was passiert, wenn man für eine Variable Werte einsetzt, die einem bestimmten Wert immer näherkommen. Dabei steht unter dem „lim“ die Variable und gegen welche Zahl sie geht (also welchem Wert die Variable immer näherkommt). Nach dem „lim“ steht dann die Funktion, worin dann die Werte für x eingesetzt werden, zum Beispiel:
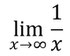
Diese Schreibweise bedeutet, dass man für x in die Funktion 1/x Werte einsetzt, immer näher an unendlich rankommen. Man kann ja keinen unendlichen Wert einsetzen, aber man kann mit dem Limes „gucken“ was für unendlich rauskommen würde. Man spricht dann „Limes gegen unendlich“. Das geht natürlich auch mit allen anderen Werten, nicht nur für unendlich.
Grenzwerte im Unendlichen
Grenzwerte im unendlichen beschreiben, was mit der Funktion passiert, also an welchen Wert sich die Funktion immer mehr annähert, wenn x gegen unendlich läuft (das heißt, wenn x immer größer wird bis unendlich). Dabei kann x gegen + und - unendlich laufen, also immer kleiner oder größer werden. Es sieht dann in mathematischer Schreibweise folgendermaßen aus:


Grafisch sieht der Grenzwert dann so aus, wie hier dargestellt für x^2. Wenn man den Grenzwert für +∞ oder -∞ haben möchte, schaut man, was die Funktion "in der Richtung macht". Hier geht sie in beide Richtungen gegen unendlich.
Grenzwerte im Endlichen
Grenzwerte im Endlichen sind Werte, die die Funktion annimmt, wenn sie sich einem bestimmten Wert annähert. Dies wird häufig an Definitionslücken verwendet, um zu prüfen, was in der Nähe dieser passiert. Dabei kann man sich dem Wert von links oder rechts annähern, also von der negativen Seite an die Definitionslücke annähern oder von der positiven, denn da kommen manchmal unterschiedliche Grenzwerte raus. Das wird dann so notiert:
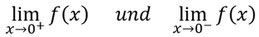
Links ist die Annäherung an Null von der positiven Seite und rechts von der negativen. Gezeichnet sieht das dann so aus:

Grafisch sieht das Ganze (für 1/x) so aus. Also man guckt, wohin die Funktion "geht", wenn man sich einmal von der positiven Seite an eine Zahl nähert und einmal von der negativen. Wie ihr seht, ergibt das 2 verschiedene Ergebnisse.
Grenzwerte bestimmen
Um einen Grenzwert zu bestimmen, muss man sich überlegen was mit der Funktion passiert, wenn man Werte einsetzt, die immer näher dem untersuchten Wert sind, also dem Wert, gegen den das x läuft.
Vorgehen für Grenzwerte gegen Unendlich
- Schaut nach, wo das x steht, z.B. im Exponenten, Nenner, Basis.... und guckt was passiert, wenn x immer größer/kleiner wird.
- Sind mehrere x da, schaut euch das x an, welches am stärksten wächst, also das, was den meisten Einfluss auf den Grenzwert hat. Z.B. hat das x mit einem höheren Exponenten mehr Einfluss, als das mit einem kleineren. Hier eine kleine Rangliste, falls mehrere x in einer Funktion vorkommen, vom kleinsten Einfluss bis zum Größten (1. kleinster Einfluss, 4. größter Einfluss):
- Wurzel von x
- x ohne Exponenten (bzw. Exponent 1)
- x mit höchstem Exponenten
- x ist selbst im Exponenten Ihr müsst dann nur gucken, was mit dem Einflussreichsten x für unendlich passiert, das ist dann der Grenzwert.
- Klammert einfach mal die höchste Potenz aus, denn überall, wo die Potenz dann im Nenner steht, wird es 0 und so seht ihr dann schnell was rauskommt.
Beispiele:

Vorgehen für Grenzwerte gegen feste Werte
Hier wird es am Beispiel von x gegen 0 erklärt:
- Setzt für jedes x Null ein und schaut, was rauskommt, dies ist manchmal bereits der Grenzwert.
- Habt ihr aber eine 0 im Nenner (was man ja nicht darf), geht es gegen unendlich, da der Nenner ja immer kleiner wird, je näher der Wert der Null kommt.
- Habt ihr aber eine 0 im Zähler und Nenner, wenn ihr für x=0 einsetzt, kommt es darauf an ob der Zähler- oder Nennergrad größer ist, bzw. wo das x mit dem größeren Einfluss ist, dieses "gewinnt" dann, also wenn Zählergrad größer ist, geht es gegen 0 und wenn Nennergrad größer gegen unendlich. Sollten jedoch auch Zähler und Nennergrad gleich sein, dann ist der Grenzwert der Quotient beider Faktoren vor dem x mit dem höchsten Exponenten im Zähler und Nenner.
Beispiele:

Grenzwerte für bestimmte Funktionen:
Potenzfunktionen
Der Grenzwert einer Potenzfunktion ist gegeben durch:
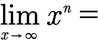
- +∞ für n>0
- 1 für n=0
- 0 für n<0
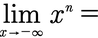
- +∞ für gerade n>0
- -∞ für ungerade n>0
- 1 für n=0
- 0 für n<0
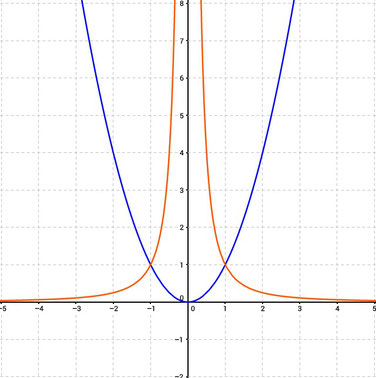
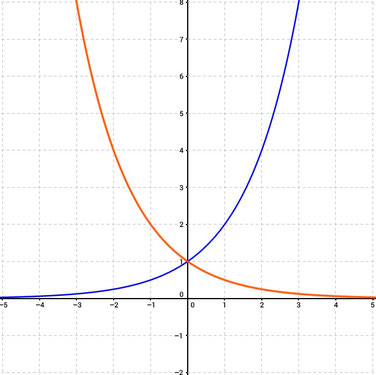
Exponentialfunktionen
Der Grenzwert der Exponentialfunktionen ist gegeben durch:
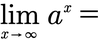
- +∞ für a>1
- 0 für a zwischen 0 und 1
- -- für a kleiner 0 gibt es keinen
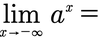
- 0 für a>1
- +∞ für a zwischen 0 und 1
- -- für a < 0 gibt es keinen
Gebrochenrationale Funktionen
Bei gebrochenrationalen Funktionen kommt es auf den höchsten Exponenten im Zähler (n) und im Nenner (m) an, aber auch auf die Faktoren vor der höchsten Potenz im Zähler (a) und Nenner (b).
Für Folgendes gilt:
- n ist der höchste Exponent im Zähler
- m ist der höchste Exponent im Nenner
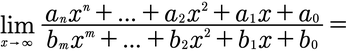
- 0 für n<m
-
an÷bm für n=m
-
+∞ für n>m und an÷bm >0
-
-∞ für n>m und an÷bm <0
Limes Rechenregeln
Hier die Rechenregeln für den Limes:
Faktorregel
Die Faktorregel sagt aus, dass man einen Faktor vor den Limes ziehen kann:

Beispiel:
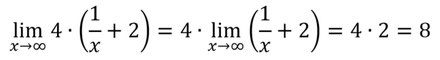
Summenregel
Die Summenregel sieht wie folgt aus:

Beispiel:

Differenzenregel
Die Differenzenregel ist genauso wie die Summenregel, nur mit einem Minus:
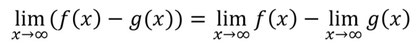
Beispiel:

Produktregel
Die Produktregel sieht wie folgt aus:

Beispiel:
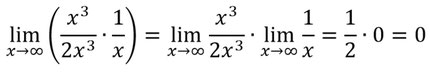
Quotientenregel
Die Quotientenregel funktioniert wie die Produktregel, nur mit der Division:

Beispiel:

Spickzettel zum Thema Grenzwerte
Hier könnt ihr euch passende Spickzettel 1.0 zum Thema Grenzwerte downloaden: