Einheitsmatrix

Die Einheitsmatrix ist eine Matrix mit speziellen Eigenschaften und besteht nur aus 1 und 0 Elementen. Für die Vektorräume der Dimensionen 1-4 sehen sie so aus:

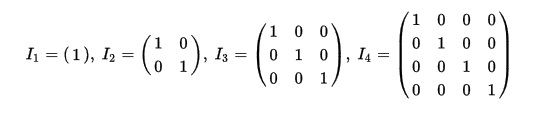
Wenn man einen Vektor eines Vekotrraums mit seiner Matrix Multipliziert kommt wieder der selbe Vektor raus. Es ist also das neutrale Element der Multiplikation eines Vektorraums. Darüber hinaus gibt es noch weitere Eigenschaften:

Neutralität: $I_m \cdot A = A \cdot I_n = A$ .
Symetrie: $(I_n)^T = I_n$
Selbstinvers: $(I_n)^{-1} = I_n$