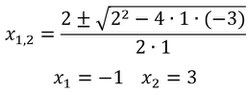Nullstellen von Funktionen berechnen
Nullstellen sind die Schnittpunkte des Graphen mit der x-Achse oder anders ausgedrückt die Werte für die eine Funktion 0 ist. Grafisch findet man also die Nullstelle dann dort (siehe Bild).
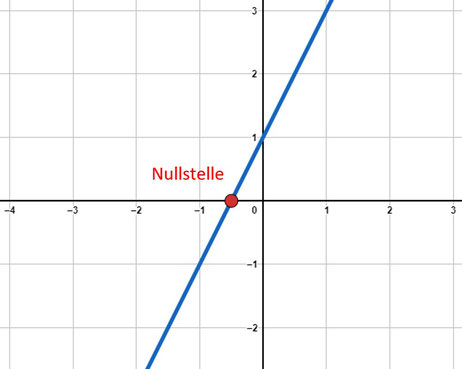
Nullstellen berechnen
Also berechnet man die Nullstellen, indem man...
- ... y=0 setzt
- ... und dann die Gleichung nach x löst (also x auf eine Seite bringen und den Rest auf die andere).
Das, was dabei raus kommt, ist dann die Nullstelle.
Dies geht vor allem bei linearen Funktionen ganz leicht. Für quadratische Funktionen gibt es die sogenannte Mitternachtsfomrel, welche weiter unten erklärt wird.
Beispiel zum Berechnen von Nullstellen
f: y=2x+1
Habt ihr eine Funktion gegeben, wie zum Beispiel diese.
0=2x+1 |-1
-1=2x |:2
-0,5=x
Ihr müsst zunächst 0 für y einsetzen und dies dann nach x auflösen, das macht ihr mit der Äquivalenzumformung.
N(-0,5|0)
Das ist dann die x-Koordinate euer Nullstelle und die y-Koordinate ist ja bei einer Nullstelle immer 0. Also ist die Nullstelle an dem Ort.
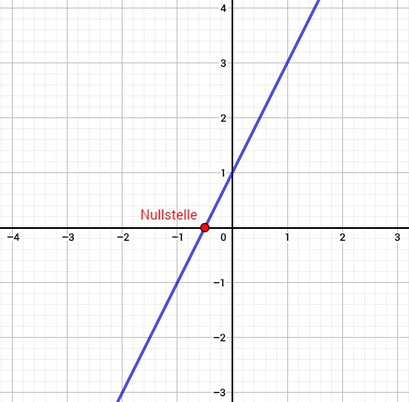
Alternativ könnt ihr es auch zeichnen und ablesen:
Beispiel zum Berechnen von Nullstellen bei quadratischen Funktion
Es sollen die Nullstellen dieser Funktion berechnet werden.
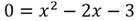
Setzt y=0.
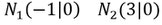
Also haben die Nullstellen diese Koordinaten.
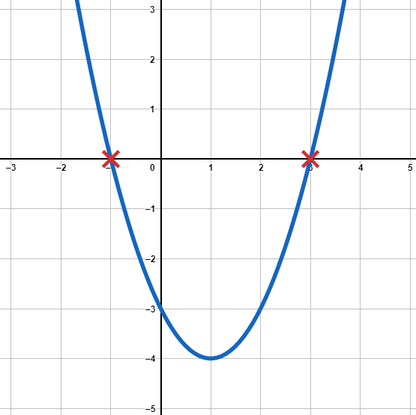
Gezeichnet sieht diese Funktion so aus:
Aufgaben zum Berechnen von Nullstellen
Hier findet ihr Übungsaufgaben, bzw. weitere Beispiele mit Lösungsweg, klickt auf Einblenden, um die Lösung zu sehen:
| Was ist die Nullstelle von f(x)=x+1? | Einblenden | |
| Was ist die Nullstelle von f(x)=-4x+8? | Einblenden | |
| Was ist die Nullstelle von f(x)=x2-9? | Einblenden | |
| Was ist die Nullstelle von f(x)=x3-27? | Einblenden | |
Tipps für verschiedene Funktionstypen
- Lineare Funktionen: y=0 setzen und nach x umformen.
- Quadratische Funktionen: y=0 setzen und mit der Mitternachtsformel die Nullstellen ausrechnen.
- Polynomfunktion: y=0 setzen und wenn nötig mit der Polynomdivision ausrechnen.
- Sinus, Cosinus und Tangens
- Gebrochenrationale Funktionen: Nullstellen vom Zähler berechnen (das sind auch die Nullstellen der Funktion).
Mitternachtsformel zum Lösen von quadratischen Gleichungssystemen
Die Mitternachtsformel ist eine Formel um quadratische Gleichungen der Form 0=ax2+bx+c lösen zu können. Wenn ihr also eine Gleichung habt die so aussieht, dann erhaltet ihr die Nullstellen in dem ihr die Zahlen a, b und c in folgende Formel einsetzt:
Weitere passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
