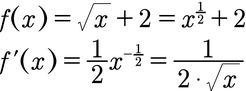Wurzelfunktion
Die Wurzelfunktion ist eine Funktion, bei der das x unter einer Wurzel steht, also so:
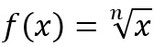
Beispiele für Wurzelfunktionen
Vorwissen zur Wurzel
Ihr müsst natürlich die Wurzel kennen, um mit der Wurzelfunktion arbeiten zu können. Hier findet ihr alles zur Wurzel:
Eigenschaften der Wurzelfunktion
Definitionsmenge und Wertemenge der Wurzelfunktion
Die Definitionsmenge und Wertemenge der Wurzelfunktion hängt davon ab, ob der Wurzelexponent gerade oder ungerade ist:
Für gerade Wurzelexponenten:
- Definitionsmenge D=ℝ0+=[0;∞[ (vorausgesetzt die Funktion wurde nicht nach links oder rechts verschoben)
- Wertemenge W=ℝ0+=[0;∞[ (vorausgesetzt die Funktion wurde nicht nach oben oder unten verschoben).
Für ungerade Wurzelexponenten:
- Definitionsmenge D=ℝ
- Wertemenge W=ℝ
Nullstellen der Wurzelfunktion
Die Nullstelle ist bei Null, falls die Funktion nicht nach oben oder unten verschoben wurde (Artikel zu Nullstellen).
Monotonie der Wurzelfunktion
Die Wurzelfunktion ist streng monoton steigend. Mehr zu dem Thema Monotonie.
Grenzwerte der Wurzelfunktion
Der Grenzwert der Wurzelfunktion für x gegen Unendlich ist Unendlich. Mehr zu dem Thema Grenzwerte.
Ableitung der Wurzelfunktion
Um die Ableitung der Wurzelfunktion zu bestimmen, formt ihr am besten die Wurzel als Exponenten um und geht dann so vor wie bei der Potenzfunktion:
- Also zieht den Exponenten vor das x
- Zeiht eins vom Exponenten am x ab
Beispiel:
Relevante Themen zur Wurzelfunktion
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
