Baumdiagramm und Pfadregeln
Ein Baumdiagramm ist ein Hilfsmittel, um Experimente und Wahrscheinlichkeiten zu veranschaulichen. Hier erklären wir euch, wie ihr dieses Hilfsmittel richtig nutzt.
Nutzen könnt ihr ein Baumdiagramm am besten, wenn ein Zufallsexperiment aus mehreren Stufen besteht. Das Baumdiagramm verdeutlicht euch die verschiedenen möglichen Ergebnisse und die Wahrscheinlichkeiten.
Hier seht ihr den Aufbau eines Baumdiagramms. Darin wird aufgetragen, was alles passieren kann, also zunächst, ob Ereignis A oder B eintritt, mit den Wahrscheinlichkeiten für A (P(A)) und für B (P(B)).
Danach die Ereignisse, die danach zutreffen können, zum Beispiel noch mal A oder B, mit den Wahrscheinlichkeiten:
- für A, nachdem davor schon A eingetroffen ist (PA(A)),
- für B, nachdem davor schon A eingetroffen ist (PA(B)),
- für A, nachdem davor schon B eingetroffen ist (PB(A)),
- für B, nachdem davor schon B eingetroffen ist (PB(B)).
Diese Wahrscheinlichkeiten nennt man dann bedingte Wahrscheinlichkeiten, da davor bereits ein anderes Ereignis eingetroffen sein muss.
Darunter steht dann die Wahrscheinlichkeit, dass beide Ereignisse nacheinander eintreffen, diese nennt man "Undwahrscheinlichkeit".
Natürlich kann es auch mehr Zweige/Äste, also Ereignisse, geben und auch noch weiter gehen, dies ist nur eine Veranschaulichung.
Die Pfadregeln - Wahrscheinlichkeiten im Baumdiagramm berechnen
1. Pfadregel
Diese besagt, dass man alle Wahrscheinlichkeiten eines Zweigs multiplizieren muss, um die "Undwahrscheinlichkeit" zu berechnen, also die Wahrscheinlichkeit, dass genau diese Ereignisse nacheinander stattfinden. Umstellen mit der Äquivalenzumformung ist natürlich möglich, falls ihr was anderes wissen möchtet.
P(A∩B) = PA(B) · P(A)
2. Pfadregel
Möchtet ihr die Wahrscheinlichkeit für eine Kombination von möglichen Ausgängen des Experiments wissen, z.b. dafür, dass zweimal Ereignis A hintereinander eintritt und das zweimal Ereignis B eintritt, dann müsst ihr die Wahrscheinlichkeit addieren.
P(A∩B)+P(A∩A)
(Wahrscheinlichkeit, dass entweder der erste oder zweite Pfad zutrifft)
Beispiel: Baumdiagramm Wahrscheinlichkeiten berechnen
Aufgabe: Ihr würfelt 2 mal einen Würfel, wie hoch ist die Wahrscheinlichkeit 2 mal hintereinander eine 1 zu würfeln?
Hier seht ihr das Baumdiagramm für diese Aufgabe. Ihr wollt die Ereignisse bei zweifachem Würfeln wissen, ob eine 1 gewürfelt wird oder nicht. Also ist auf dem einen Zweig des Baumdiagramms das Ereignis "es wird eine 1 gewürfelt" und auf dem anderen das Ereignis "es wird keine 1 gewürfelt", dieses Ereignis wird einfach genauso benannt, wie das andere Ereignis, nur mit einem Strich darüber, dieser bedeutet, dass damit das Gegenteil gemeint wird, also das Gegenereignis, in dem Fall "keine 1".
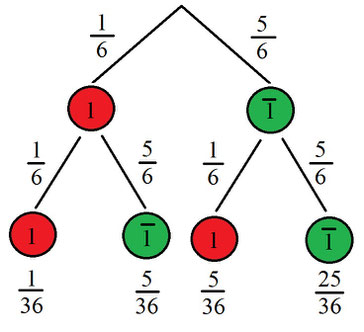
Wie ihr seht, stehen die jeweiligen Wahrscheinlichkeiten an den Zweigen, welche zu dem Ereignis führen. Die Wahrscheinlichkeiten unten (Undwahrscheinlichkeiten) wurden mit der 1. Pfadregel berechnet, also alle Wahrscheinlichkeiten dieses Zweigs multipliziert.
Lösung: Die Wahrscheinlichkeit 2 mal hintereinander eine 1 zu würfeln liegt bei 1/36.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
