Exponentielles Wachstum und Zerfall

Exponentielles Wachstum und Zerfall kommt häufig vor, beispielsweise bei Bakterien, Radioaktivität und Medikamenteneinnahme. Hier erkläre ich euch alles Wichtige dazu.

Zunächst zu der allgemeinen Form:

• N₀ ist der Anfangsbestand

• a die Änderungsrate, also wie stark sich der Bestand mit der Zeit verändert
• t ist die Zeit

Ob es ein Zerfall oder Wachstum ist, erkennt ihr am a:

• ist a > 1, ist es ein exponentielles Wachstum
• ist a < 1, ist es eine exponentielle Abnahme

Prozentuale Abnahme oder Zunahme am a Ablesen:

• ist a > 1, müsst ihr a-1 rechnen und ihr erhaltet die prozentuale Zunahme. z.B. 1,3-1=0,3=30%
• ist a < 1, müsst ihr 1-a rechnen und ihr erhaltet die prozentuale Abnahme. z.B: 1-0,8=0,2=20%

Exponentielle Ab- und Zunahme bedeutet, dass sich die Anzahl nicht gleichmäßig verändert, also immer um dieselbe Anzahl z.B. pro Stunde, sondern sich immer um einen bestimmten Faktor verändert, also z.B. sich alle 2 Stunden verdoppelt. Das wollen wir euch nun mal an einem Beispiel verdeutlichen:

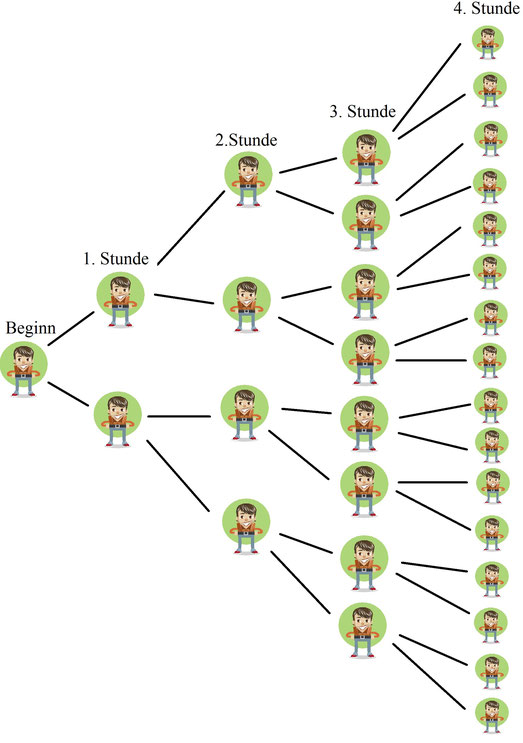
Nehmen wir mal an, dass anfangs nur eine Person ein Hipster war, aber jeder Hipster schafft es pro Stunde eine weitere Person zu einem Hipster zu machen.

Übersicht:

1. Wachstumsfaktor a gesucht
   • Prozentangabe bekannt (berechnen der Wachstumsrate pro Stunde, wenn z.B. pro 3 Studen in Prozent gegeben ist)
   • Anzahl der Zunahme/Abnahme bekannt
2. Startwert N₀ gesucht
3. Zeit t gesucht
4. Halbwertszeit/Verdopplungszeit gesucht

Habt ihr das Wachstum oder den Zerfall in der Angabe bereits in Prozent gegeben, geht es relativ leicht. Addiert (bei Wachstum) oder subtrahiert (bei Abnahme) die Prozentangabe an/von 1. Das ist dann der Wachstumsfaktor für die dazu angegebene Zeit in der sich die Anzahl um diesen Prozentsatz verändert. (Wiederholung zur Prozentrechnung)

Beispiel:

Bakterien vermehren sich in 3 Stunden um 30%. Wie groß ist der Wachstumsfaktor für 1 Stunde?

Lösung:

1. Da es ein Wachstum ist, addiert ihr die 30% zu 100%, da es ja um 30% wächst, also ist der Wert nach drei Stunden 130% von dem ursprünglichen Wert:

2. Nun habt ihr den Wachstumsfaktor für 3 Stunden gegeben und könnt so eure Wachstumsgleichung aufstellen, vergesst aber nicht, dass diese Zunahme in 3 Stunden passiert, weshalb ihr die Zeit durch 3h teilen müsst. Es sind ja 30% pro 3 Stunden:

3. Möchtet ihr nun das Wachstum für eine Stunde wissen, könnt ihr die Potenzgesetzte anwenden und das "hoch ein Drittel" ausklammern und hoch die Zeit nehmen. Das in der Klammer könnt ihr dann ausrechnen. Das ist dann euer Wachstumsfaktor a für eine Stunde:

Nun seid ihr fertig. Ihr könnt nun auch ablesen, dass die Bakterienanzahl pro Stunde um 9,1% zunimmt.

Habt ihr die Anzahl der Zunahme bzw. Abnahme gegeben, könnt ihr entweder, wie oben, die prozentuale Zunahme oder Abnahme ausrechnen und dann wie oben vorgehen oder ihr macht es so:

Beispiel:

Anfangs sind noch 1000 HSV-Fans zuversichtlich, dass sie in der Bundesliga bleiben, allerdings sind es nach 30 Minuten nur noch 300. Wie ist die Gleichung der exponentiellen Abnahme und wie viel Prozent verlieren pro Minute den Glauben?

Lösung:

1. Da ihr den Anfangswert und die Zeit gegeben habt, könnt ihr in die Gleichung einsetzen:

2. Dies formt ihr dann nach a um (Wiederholung zur Äquivalenzumformung):

3. Jetzt seid ihr fast fertig, um die Prozentzahl zu ermitteln, müsst ihr nur 1-a (bei Zerfall, a-1 bei Zunahme) rechnen:

Jetzt seid ihr fast fertig, um die Prozentzahl zu ermitteln, müsst ihr nur 1-a (bei Zerfall, a-1 bei Zunahme) rechnen, also hier 4% pro Minute nimmt die Anzahl an HSV-Fans, die an den Klassenerhalt glauben, ab.

Ist der Startwert N₀ gesucht, geht ihr so vor:

Beispiel:

Nach 2 Jahren sagen nur noch 500 Schüler der Waldorfschule "Babo" zueinander. Die Anzahl fällt jährlich um 60%. Wie viele Schüler haben vor 2 Jahren "Babo" zueinander gesagt?

Lösung:

1. Setzt alles in die Gleichung ein, was ihr wisst, das a erhaltet ihr, indem ihr eins minus die Prozentzahl rechnet, also 1-0,6=0,4:

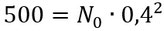
2. Formt das nur noch um und ihr habt den Startwert:

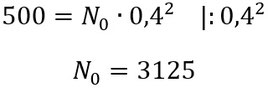
Es haben also anfangs 3125 Schüler "Babo" zueinander gesagt. Eine alarmierend hohe Zahl.

Sucht ihr die Zeit t, dann geht ihr so vor:

Beispiel:

Der Hype um ein YouTube Video hat exponentiell zugenommen. Die Klicks sind pro Stunde um 30% gestiegen! Anfangs waren es nur 2 Stück. Wie lange dauerte es bis, es 100.000 wurden?

Lösung:

1. Setzt erst mal alles in die allgemeine Gleichung ein:

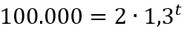
2. Formt es nach t um:

Wie ihr seht hat das Video dann nach nur 41,24 Stunden 100.000 Klicks! Das sind nicht einmal 2 Tage.

Die Halbwertszeit/Verdopplungszeit ist die Zeit, nach welcher sich ein Wert halbiert/verdoppelt hat. Ist die Halbwertszeit oder Verdopplungszeit gesucht, geht ihr so vor:

Beispiel:

Der Sieger des Jungle-Camps ist anfangs sehr bekannt, aber schon nach kurzer Zeit kennt ihn keiner mehr. Die Bekanntheit nimmt pro Tag um 5% ab. Wie lang ist die Halbwertszeit?

Lösung:

1. Setzt alles, was ihr wisst, in die Gleichung ein (wie man a berechnet, findet ihr weiter oben), vergesst nicht, dass ihr auch eine Anzahl wisst, nämlich ist der Endwert nach der Halbwertszeit noch die Hälfte des Startwerts (Das große T ist die Halbwertszeit):

2. Formt es nach T (der Halbwertszeit) um:

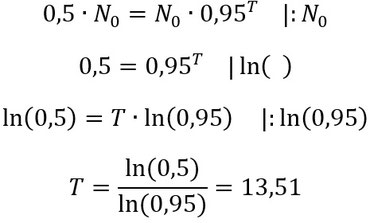
Das ist dann eure Halbwertszeit. Also die Halbwertszeit des Jungle-Königs sind 13,51 Tage.

• Exponentialfunktion
• Logarithmus
• Potenzen
• Potenzgesetze