Trigonometrische Funktionen
Den Kosinus, Sinus und Tangens kennt ihr sicherlich schon aus der Geometrie. Hier werden nun die Funktionen dieser Operatoren vorgestellt.
Sinusfunktion
Die Sinusfunktion sieht folgendermaßen aus:
y=sin(x)
Der Graph des Sinus ist die sogenannte Sinuskurve, hier die wichtigsten Eigenschaften:
- Die Sinuskurve ist periodisch mit einer Periode von 2π. (Das bedeutet nach 2π beginnt sie wieder von vorne). Daraus folgt: sin(x)=sin(x+2π)
- Bei x=0 ist die Sinusfunktion 0 (also sie beginnt bei 0)
- Die Nullstellen sind bei ganzzahligen Werten von π, also π, 2π, 3π, 4π....
- Der Graph schwankt zwischen -1 und 1. Die Hoch- und Tiefpunkte sind bei π/2, also bei π/2, 2π/2, 3π/2....
- Definitionsbereich: D=ℝ
- Wertebereich: W=[-1;1]

Kosinusfunktion
Die Kosinusfunktion sieht folgendermaßen aus:
y=cos(x)
Der Graph der Kosinusfunktion ist die Kosinuskurve mit folgenden Eigenschaften:
- So wie die Sinusfunktion ist auch die Kosinusfunktion periodisch mit der Periode 2π -> cos(x)=cos(x+2π)
- Bei x=0 ist die Kosinusfunktion 1, also genau andersrum als die Sinusfunktion
- Die Nullstellen sind genau da, wo die Hoch- und Tiefpunkte der Sinusfunktion sind, also bei π halben.
- Die Hoch- und Tiefpunkte der Kosinusfunktion sind an den Nullstellen der Sinusfunktion, also an ganzzahligen Vielfachen von π.
- Definitionsbereich: D=ℝ
- Wertebereich: W=[-1;1]

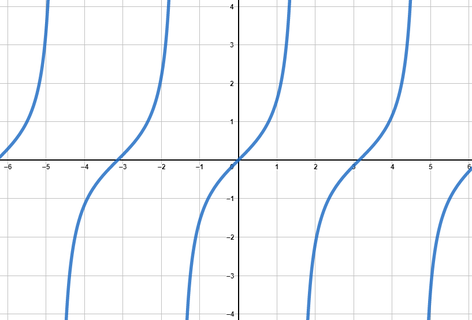
Tangensfunktion
Die Tangensfunktion ist folgendermaßen definiert:
y=tan(x)
dabei ist der Tangens eine Zusammensetzung der Sinus- und Kosinusfunktionen, nämlich der Quotient von Sinus und Kosinus:

Mit diesem Wissen lassen sich die Nullstellen und Definitionslücken leicht bestimmen:
- Nullstellen der Tangensfunktion sind dieselben wie bei der Sinusfunktion
- Definitionslücken sind an den Stellen, an denen die Kosinusfunktion 0 ist, da man ja nicht durch 0 teilen darf. Also an den Nullstellen der Kosinusfunktion.
- Die Periode ist genauso wie bei der Cosinus- und Sinusfunktion π
- Definitionsbereich: D=ℝ\{(ℤ+1/2)·π} (das bedeutet einfach, dass im Definitionsbereich ganz ℝ ist, außer alle vielfachen von π, die durch einhalb geteilt werden können. Also anders gesagt es ist überall definiert außer an den Nullstellen der Kosinusfunktion.)
- Wertebereich: W=ℝ
Funktionen modulieren
Allgemein kommen die Funktionen eher selten in der reinen Form wie oben vor sondern eher in der Form:
y=a·sin(bx+c)+d
y=a·cos(bx+c)+d
- a gibt die Amplitude an, also den höchstmöglichen Wert, wenn er 1 ist (wie in der Form von ganz oben), dann schwankt die Amplitude zwischen 1 und -1. Wäre a=2 so würde die Funktion zwischen 2 und -2 schwanken. (Probiert es doch mal aus im Graph Zeichner oben ;))
- b verändert die Periode. Je größer b, umso kürzer ist die Periode, also desto gestauchter ist die Funktion
- c verschiebt die Funktion nach links und rechts, ist c>0 so wird die Funktion nach links verschoben und ist c<0 wird sie nach rechts verschoben
- d verschiebt die Funktion nach oben oder unten, wie ihr es schon aus linearen Funktionen kennt, dort heißt es dann meist t ;)
Ableitungen der jeweiligen Funktionen
Ableitung der Sinusfunktion:

Ableitung der Cosinusfunktion:

Ableitung der Tangensfunktion:

