Satz des Pythagoras
Der Satz des Pythagoras ist eine Möglichkeit die Länge von Seiten in einem rechtwinkligen Dreieck berechnen zu können. Wichtig dabei ist, dass es wirklich nur bei Dreiecken mit einem rechten Winkel geht. Die Formel sieht dann so aus (ihr könnt dann natürlich mit der Äquivalenzumformung die Formel umstellen, um zum Beispiel a oder b auszurechnen):
a2+b2=c2
- a ist eine Kathete
- b ist die andere Kathete
-
c ist die Hypotenuse (gegenüber vom rechten Winkel)
Wenn ihr zwei dieser Längen wisst, könnt ihr die andere Länge berechnen. Stellt einfach die Gleichung um und setzt ein. Der Satz des Pythagoras besagt auch, dass die quadratischen Flächen der Katheten (also die Flächen von Quadraten mit den Seitenlängen a und b zusammen genauso groß sind, wie die Fläche eines Quadrats mit der Seitenlänge c. a2 ist ja die Fläche eines Quadrats mit Länge a.
Beispiel: Satz des Pythagoras berechnen
Ihr möchtet die Länge von b wissen, und wisst, dass a=3cm und c=4cm sind. Lasst euch dabei nicht von der Beschriftung verwirren, hier ist b die Hypotenuse, da b gegenüber vom rechten Winkel liegt. Also gilt mit dem Satz des Pythagoras:
Also rechnet ihr dann:
Dann nicht vergessen die Wurzel zu ziehen, da das oben ja quadriert ist:
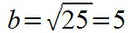
Also ist b 5cm lang.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
