Sinus, Cosinus und Tangens + Einheitskreis
Erklärungen zur Sinus-, Cosinus- und Tangensfunktion findet ihr im Artikel "trigonometrische Funktionen".
Mit dem Sinus, Cosinus und Tangens könnt ihr in rechtwinkligen Dreiecken mit Winkeln rechnen.
Dabei müsst ihr wissen, wo die Hypotenuse und die An- und Gegenkathete liegen. In diesem Bild seht ihr es, die Hypotenuse ist gegenüber des rechten Winkels, die Ankathete ist am Winkel, den ihr berechnen wollt, und die Gegenkathete ist gegenüber dem Winkel, welchen ihr berechnen wollt.
Sinus berechnen
Mit dem Sinus könnt ihr den Winkel in einem rechtwinkligen Dreieck berechnen oder, wenn ihr den Winkel gegeben habt, die Gegenkathete oder Hypotenuse. Der Sinus ist immer zwischen 0 und 1:
- Der Sinus ist 1 bei 90° und 270°
- Der Sinus ist 0 bei 0° und 180°
Beispiel zum Berechnen vom Sinus
Wenn ihr in diesem Dreieck den Winkel α berechnen möchtet, könnt ihr dies mit dem Sinus machen. Teilt dazu die Gegenkathete durch die Hypotenuse:
Nun müsst ihr nur noch im Taschenrechner folgendes eingeben und ihr habt das Ergebnis:
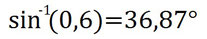
Cosinus berechnen
Mit dem Cosinus könnt ihr den Winkel in einem rechtwinkligen Dreieck berechnen oder, wenn ihr den Winkel gegeben habt, die Ankathete oder Hypotenuse. Wie der Sinus, ist auch der Cosinus immer zwischen 0 und 1:
- 1 bei 0° und 180°
- 0 bei 90° und 270°
Beispiel: Cosinus im Dreieck berechnen
Wenn ihr in diesem Dreieck den Winkel α berechnen möchtet, könnt ihr dies mit dem Cosinus machen. Teilt dazu die Ankathete durch die Hypotenuse:
Nun müsst ihr nur noch im Taschenrechner folgendes eingeben und ihr habt das Ergebnis:
Tangens berechnen
Mit dem Tangens könnt ihr den Winkel eines rechtwinkligen Dreiecks berechnen, wenn ihr die Gegenkathete und Ankathete kennt.
Beispiel: Tangens im Dreieck berechnen
Wenn ihr in diesem Dreieck den Winkel α berechnen möchtet, könnt ihr dies mit dem Tangens machen. Teilt dazu die Gegenkathete durch die Ankathete:
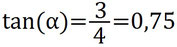
Nun müsst ihr nur noch im Taschenrechner folgendes eingeben und ihr habt das Ergebnis:
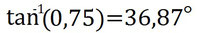
Sinus und Cosinus im Einheitskreis
Im Einheitskreis kann man die Werte von Cosinus und Sinus direkt ablesen, da die Hypotenuse 1 ist und somit ist dann die Länge der Ankathete gleich dem Cosinus und die Länge der Gegenkathete ist gleich dem Sinus (es wird ja schließlich bei beiden durch die Hypotenuse geteilt, da diese beim Einheitskreis immer 1 ist, ist die Ankathete gleich dem Cosinus und die Gegenkathete gleich dem Sinus). Wie ihr dann seht, ist der Cosinus maximal bei einem Winkel von 0° und 180° und minimal bei einem Winkel von 90° und 270°.
Hier könnt ihr mal probieren, wie sich die Sinus- und Cosinuswerte für bestimmte Winkel ändern, indem ihr den Schieberegler verschiebt. Es werden euch gleich die Werte für Sinus und Cosinus für diesen Winkel angezeigt.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
