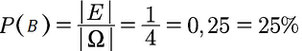Laplace Experiment / Versuch
Ein Laplace Experiment ist ein Zufallsexperiment, wobei jedes Ergebnis dieselbe Wahrscheinlichkeit hat. Dies ist zum Beispiel bei einem Würfel der Fall, da die Wahrscheinlichkeit eine eins zu würfeln genauso hoch ist, wie die restlichen Ergebnisse.
Beispiele für Laplace Experimente sind:
- Würfeln
- Münze werfen
- Eine von 5 unterschiedlichen Kugeln ziehen
- ...
Die Formel zur Berechnung der Wahrscheinlichkeit eines Laplace Experiments ist:
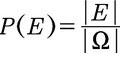
Dabei ist:
- |E| die Anzahl an Ergebnissen, bei denen euer Ereignis zutrifft.
-
- Beim Ereignis die 1 würfeln, gibt es nur eine Möglichkeit, nämlich wenn der Würfel die 1 anzeigt, deshalb würde dann die 1 an der Stelle stehen.
- Beim Ereignis eine gerade Zahl würfeln, gibt es 3 Möglichkeiten, die 2, 4 und 6. Deshalb kommt dann bei diesem Beispiel eine 3 an diese Stelle.
- |Ω| ist die Anzahl an allen möglichen Ergebnissen des Zufallsexperiments.
-
- Beim Würfeln wäre es 6, da es 6 mögliche Ergebnisse beim Würfeln gibt.
- Beim Münze werfen wäre es 2, da nur Kopf und Zahl möglich sind
Aufgabe zum Laplace Experiment
Klickt auf einblenden, um die Lösung der Aufgabe zu sehen.
| Wie groß ist die Wahrscheinlichkeit eine gerade Zahl zu würfeln? | Einblenden | |
Beispiel zum Laplace Experiment
Ihr werft 2 mal eine Münze und sollt folgende Wahrscheinlichkeiten berechnen:
- Ihr werft mindestens einmal Kopf (Ereignis A), also entweder einmal oder zweimal
- Ihr werft zweimal Kopf (Ereignis B)
Das berechnet ihr so:
Lösung zu 1.
- Bestimmt, wie viele Ergebnisse auf die Forderung zutreffen, das macht ihr entweder, indem ihr euch die Möglichkeiten aufschreibt, oder ihr rechnet es aus:
- Aufgeschrieben wäre es (K steht für Kopf und Z für Zahl): A={ZK; ZZ; KZ} -> es sind 3 Möglichkeiten
- oder, um es zu berechnen, schaut euch noch mal unser Kapitel Anzahl der Möglichkeiten berechnen an.
- Dann bestimmt man die Anzahl an allgemein möglichen Ergebnissen, also wie viele mögliche Ergebnisse gibt es beim zweimaligen Münzwurf (z.B.
Kopf-Kopf, Zahl-Kopf, Zahl-Zahl...),
- das macht man, entweder, indem man sich alle Möglichkeiten aufschreibt -> Es gibt insgesamt 4 Möglichkeiten.
- oder, indem man die Anzahl an Möglichkeiten pro Wurf (also 2) hoch die Anzahl an Würfen (hier auch 2) nimmt -> Es gibt insgesamt 4 Möglichkeiten beim zweifachen Münzwurf.
- danach teilt man die Anzahl an Ergebnissen, die eure Bedingung erfüllen, durch die gesamt mögliche Anzahl an Ergebnissen, dann erhaltet ihr für die Wahrscheinlichkeit:
Wie ihr seht, ist die Wahrscheinlichkeit mindestens einmal Kopf zu werfen bei 75%. Alternativ könnt ihr auch einfach die Wahrscheinlichkeit das genau 1 mal Kopf raus kommt (50%) mit der Wahrscheinlichkeit das genau 2 mal Kopf raus kommt (25%) addieren. Denn das sind die beiden Möglichkeiten, dass mindestens einmal Kopf dabei ist.
Lösung zu 2.
Geht wie oben vor dann erhaltet ihr:
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
