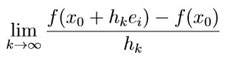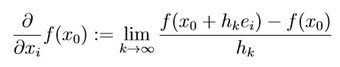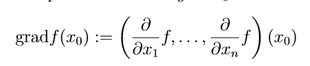Differentialrechnung
Definition:
Sei M⊂ℝn und x0∈M, f : M→ℝ. {e1,...,en} sei die Standard-Orthonormalbasis (gibt die Richtung an zb. x-Richtung) des ℝn. Sei i ∈ {1,...,n}. Für jede Nullfolge (hk)k∈ℕ mit der Eigenschaft, dass hk ≠0 für alle k∈ℕ ist, existiere der Grenzwert
Dann heißt f in x0 partiell differenzierbar bezüglich der Richtung ei, und
heißt partielle Ableitung von f in Richtung ei.
Bemerkung:
- Fall n = 1. Wir benutzen die Schreibweise
Geometrisch beschreibt f´(x0) die Steigung der Tangente an den Graph von f im Punkte (x0,f(x0)).
-
Fall n > 1. Wir fassen die partielle Ableitung in x0 in einem Vektor
zusammen, der Gradient von f in x0 heißt. Andere Schreibweise:
Bemerkung:
Stetigkeit impliziert im Allgemeinen nicht Differenzierbarkeit. Als Gegenbeispiel betrachten wir f(x) = |x|. Diese Funktion ist in x0=0 stetig, aber nicht differenzierbar.
Satz 1 (Produktregel, Quotientenregel):
Sei x0∈M, M ⊂ R, f,g : M→ℝ seien in x0 differenzierbar. Dann gilt:
-
f + g : M→ℝ ist in x0 differenzierbar mit (f + g)´(x0) = f´(x0) + g´(x0).
-
Produktregel: f ·g : M→ℝ ist in x0 differenzierbar mit (f ·g)´(x0) = f´(x0)g(x0) + f(x0)g´(x0).
-
Quotientenregel: Falls g(x0)≠0, so ist f /g : {x ∈ M|g(x)≠0}→ℝ in x0 differenzierbar mit:
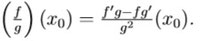
Satz 2 (Kettenregel):
Sei x0∈M, M⊂ℝ . f : M → ℝ sei in x0 differenzierbar. g : K → ℝ sei differenzierbar in f(x0), f(M) ⊂ K und f(x0) sei innerer Punkt von K. Dann ist g ◦f in x0 differenzierbar und es gilt
(g◦f)´(x0) = g´(f(x0))·f´(x0).
Definition:
f : M → ℝ heißt n-mal (stetig) differenzierbar, falls f(n) für n∈ℕ existiert und stetig ist.