Lineare Funktion
Eine lineare Funktion ist eine Funktion mit konstanter Steigung der Form:
y=mx+t
- Dabei gibt m die Steigung an
-
- je größer m ist, desto steiler steigt/fällt die Funktion
- ist m positiv, steigt die Funktion
- ist m negativ, fällt die Funktion
- t den y-Achsenabschnitt. (also den Schnittpunkt mit der y-Achse)
- f(x)=y Lasst euch nicht verwirren, falls euer Lehrer f(x) statt y schreibt, das bedeutet dasselbe.
Beispiele von linearen Funktionen
y=x+1
y=3x
y=-x+2
Nullstellen
Die Erklärung wie man Nullstellen genau berechnet, findet ihr unter Nullstellen.
Liegt ein Punkt auf einer Geraden?
Wenn ihr wissen wollt, ob ein Punkt auf der Geraden liegt, setzt ihr die Koordinaten des Punktes in die Gleichung ein, wenn die Gleichung dann stimmt (also wenn links und rechts dieselbe Zahl rauskommt), liegt der Punkt auf der Geraden, wenn nicht liegt er daneben.
Beispiel:
Gegeben ist der Punkt P(1I3) und die Funktion f: y=x+2
- Man setzt den Punkt in die Gleichung ein: 3=1+2
- -> Der Punkt liegt auf der Geraden, da die Gleichung aufgeht 3=3.
Aufgaben zum Üben
| Liegt der Punkt P(3|4) auf der Geraden f(x)=x+1? | Einblenden | |
| Liegt der Punkt A(4|1) auf der Geraden f(x)=4x-1? | Einblenden | |
Wie berechne ich die Steigung?
Die Steigung kann man auf verschiedene Arten lösen, je nachdem was gegeben ist:
1. Zwei Punkte sind gegeben:
Wenn man zwei Punkte (nennen wir sie mal P1(x1Iy1) und P2(x2Iy2)) gegeben hat, kann man die Steigung folgendermaßen berechnen:
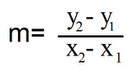
Beispiel:
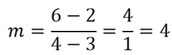
2. Der Graph ist gegeben:
Wenn der Graph gegeben ist, sucht man sich einfach zwei Punkte und dann macht man es wie bei 1.. Oder man macht es mit dem Steigungsdreieck. Wählt euch dazu einen Punkt aus und geht eine bestimmte Länge (eine mit der ihr einfach rechnen könnt, also z.B. 1 oder 2) nach unten und teilt das durch die Länge, die ihr nach links oder rechts gehen müsst, um wieder beim Graphen zu sein. Wenn ihr nach links geht, ist die Steigung positiv, wenn nach rechts dann negativ:
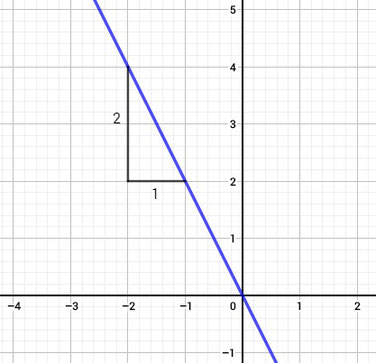
Negative Steigung, da 2 nach unten und dann nach rechts. Hier ist die Steigung -2, da -2:1=-2 ist.
Positive Steigung, da 2 nach unten und dann nach links. Hier ist die Steigung 2, da 2:1=2 ist.
3. Steigungswinkel ist gegeben:
Wenn der Steigungswinkel des Graphen gegeben ist, lässt sich diese berechnen durch:
m=tan α
4. Gerade senkrecht auf einer Anderen:
Ist eine Gerade senkrecht auf einer Anderen, von der ihr die Steigung wisst, dann kann man die Steigung der senkrechten Gerade berechnen durch:
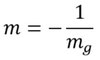
Dabei ist mg die gegebene Steigung der Geraden, auf welcher die andere dann senkrecht sein soll.
Beispiel:
Welche Steigung ist senkrecht zu dieser Steigung?:
So lässt sich dann die senkrechte Steigung berechnen:
Aufgaben zur Steigung
| Eine Gerade geht durch die Punkte A(1|1) und B(2|2). Wie groß ist die Steigung? | Einblenden | |
| Eine Gerade geht durch die Punkte A(0|1) und B(1|3). Wie groß ist die Steigung? | Einblenden | |
Wie ermittel ich die Funktionsgleichung?
- Zunächst ermittelt ihr die Steigung, das geht mit den oben beschriebenen Methoden.
- Wenn ihr die Steigung habt, setzt ihr einen Punkt, den ihr kennt und wisst, dass er auf dem Graphen liegt, in die Gleichung y=mx+t ein.
- Ihr kennt dann ja y, m und x, dann müsst ihr nur noch nach t auflösen, dann habt ihr t.
- Danach setzt ihr nur noch in die Gleichung m und t ein und ihr habt die Funktionsgleichung.
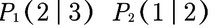
- Ihr habt beispielsweiße diese beiden Punkte gegeben und möchtet die Funktionsgleichung wissen.
- Berechnet dann zunächst die Steigung, wie im Punkt darüber beschrieben.
- Setzt einen Punkt und die Steigung in die allgemeine Funktionsgleichung ein und löst das nach t auf.
- Setzt jetzt m und t in die allgemeine Funktionsgleichung ein und ihr seid fertig.
Aufgaben zur Funktionsgleichung
| Eine Gerade geht durch die Punkte A(0|1) und B(1|3). Was ist ihre Funktionsgleichung? | Einblenden | |
| Eine Gerade geht durch die Punkte A(1|1) und B(2|2). Was ist ihre Funktionsgleichung? | Einblenden | |
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
