Linearkombinationen und lineare Unabhängigkeit
Linearkombination
Eine Linearkombination ist eine Kombination von Vektoren mit Skalarmultiplikationen, welche addiert werden und so neue Vektoren ergeben. So kann man also neue Vektoren "erschaffen" bzw. "bauen". Hier die allgemeine Form der Linearkombination, wobei λ einfach immer eine Zahl ist und v ein Vektor:
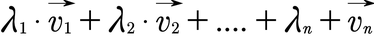
Beispiel zur Berechnung der Linearkombination

Lineare Unabhängigkeit
Lineare Unabhängigkeit bedeutet, dass Vektoren sich nicht wie oben aus anderen Vektoren zusammenbauen lassen. Habt ihr also 3 Vektoren und der 3. Vektor lässt sich aus den anderen beiden wie oben gezeigt zusammenbauen, dann ist dieser nicht linear unabhängig, sondern linear abhängig den anderen Vektoren gegenüber. Wie überprüft man auf lineare Unabhängigkeit?:
- Wenn die Determinante der Vektoren 0 ist, sind sie linear abhängig.
- Probiert einfach aus, ob ihr den Vektor aus den anderen beiden "bauen könnt".
