Mit Mathe in die Zukunft sehen

Habt Ihr Euch schon einmal gefragt, woher Google weiß, was Ihr als nächstes Wort in die Suchmaske eingeben wollt, oder woher Google weiß, welche Frage Ihr stellt, nachdem Ihr nur zwei Wörter eingegeben habt? Solche Vorhersagen basieren darauf in großen Datenmengen komplexe Strukturen zu identifizieren. Solche Systeme werden nicht nur von IT-Unternehmen wie Google und Facebook benötigt, sondern auch von Banken. Wenn eine Bank heute schon weiß, dass Ihr Geschäftspartner in drei Monaten insolvent wird, kann sie morgen bereits Vorkehrungen treffen.

Normalerweise bringt man Computern bei Probleme zu lösen indem man ihm eine Liste von Anweisungen einspeichert, die er Schritt für Schritt durchführt. Damit kann man sehr viele Probleme lösen und Computern sehr viel beibringen. Zum Beispiel ist so Windows entstanden, Android, iOS, oder Eure Lieblings-Anwendung auf Eurem Smartphone. Es gibt aber auch Probleme, die mit einer Liste von Anweisungen nur sehr schwer oder gar nicht lösbar sind. Versucht zum Beispiel einem Freund zu erklären, wie man auf einem Bild einen Hund von einer Katze unterscheiden kann. Dabei dürft Ihr aber Begriffe wie Augen, Ohren, Nase, Schnauze, etc. nicht verwenden. Wenn Ihr solche Begriffe verwendet, dann löst Ihr das eigentliche Problem nämlich nur insofern, dass Ihr es auf ein anderes, genauso schwieriges Problem zurückführt. Euer Freund muss nämlich Dinge wie Augen, Ohren, Nase etc. bereits erkennen können. Was müsste Euer Freund Schritt für Schritt machen, damit er das bei vielen Bildern von Hunden und Katzen schafft? Euch wird auffallen, dass es sehr schwierig ist genau zu benennen, wie man Hunde von Katzen, oder allgemein Objekte voneinander unterscheiden kann. Für solche Arten von Problemen funktioniert also die alte Strategie nicht, dem Computer eine Liste von Anweisungen zu geben mit der er das Problem löst, da der Mensch, der die Liste für den Computer erstellen soll selbst nicht weiß, wie er die Lösung des Problems in Worte fassen kann. Einem Menschen könnt ihr beibringen Hunde von Katzen zu unterscheiden indem ihr ihm/ihr viele Bilder von Hunden und Katzen zeigt und ihm jedes Mal sagt, ob es ein Hund oder eine Katze ist. Wie wäre es, wenn man einem PC sehr viele Bilder von Hunden und Katzen zeigen könnte, die alle betitelt sind mit „Hund“ oder „Katze“? Ist es möglich, dass ein PC anhand von Beispielen selber lernen kann, wie man Hunde und Katzen unterscheidet? Ja, das geht mit maschinellem Lernen.

Der Teil maschinellen Lernens mit dem man diese Art von Problemen lösen kann sind sogenannte neuronale Netze. Sie sind in ihrer Funktionsweise dem menschlichen Gehirn nachempfunden. Wie Euer Gehirn, bestehen neuronale Netze aus Neuronen, die über Leitungen miteinander verbunden sind und so miteinander kommunizieren können. Ein Neuron hat immer ein paar Eingänge, wo Signale reinfließen können und ein paar Ausgänge, woraus das Neuron Signale raussenden kann. Stellt Euch das wie elektrische Leitungen vor. Ein Neuron macht Nichts, so lange kein Signal entlang seiner Eingänge reinfließt. Fließen Signale rein wird das Neuron erregt. Übersteigt die Erregung eine gewisse Schwelle, dann feuert das Neuron entlang seiner Ausgänge Signale an andere Neuronen. Während des Lernprozesses im Gehirn, werden neue Verbindungen zwischen Neuronen aufgebaut oder abgebaut und bestehende Verbindungen verstärkt oder abgeschwächt. Dieses Verhalten von Neuronen kann man mathematisch formulieren, dadurch für Computer zugänglich machen und dann Neuronen in Netzwerken (d.h. ganz viele Neuronen die miteinander verbunden sind) simulieren. 

Bild 1: Das Bild zeigt ein einfaches Neuron und seine Funktionsweise.

In Bild 1 seht Ihr ein sehr einfaches Neuron mit zwei Eingängen und einem Ausgang. Entlang der Eingangsleitungen erhalten wir Erregungen x₁ und x₂. Die Stärke der Signalleitungen (oder deren elektrischer Widerstand) werden durch a₁ und a₂ angedeutet. Die Stärke der Leitungen beachten wir, indem wir die Erregung mit der Leitungsstärke multiplizieren. Das heißt das gesamte Eingangssignal E beträgt dann

E=a₁⋅x₁+a₂⋅x₂.

Das Neuron hat einen eigenen Schwellenwert S. Erst wenn das Eingangssignal stärker ist als der Schwellenwert wird das Neuron aktiv. Wir beobachten also, ob E≥S ist (oder nicht). Sobald E≥S ist, generieren wir ein Ausgangssignal der Stärke 1 an der Ausgangsleitung (Dies ist ein sogenanntes binäres Neuron. Wie das Ausgangssignal aussieht hängt vom Typ des Neurons ab. Zum Beispiel gibt es auch ein lineares Neuron. Ein solches Neuron gibt immer den Wert E-S an der Ausgangsleitung weiter) und leiten das Signal an das Neuron weiter, zu dem die Ausgangsleitung dieses Neurons führt. Das machen wir für alle Neuronen in unserem Netzwerk gleichzeitig. Wir müssen also immer den Überblick darüber haben wie die Neuronen untereinander verbunden sind. Das ist natürlich furchtbar unübersichtlich und kompliziert. Es gibt aber eine einfache Methode um hier nicht den Überblick zu verlieren. Dazu müssen wir uns Bild 2 anschauen. Hier sehen wir ein neuronales Netz. Die Neuronen sind hier in Gruppen eingeteilt die wir Schichten nennen. 

Bild 2: Das Bild zeigt ein neuronales Netz. Die Kreise sind Neuronen, wie sie in Bild 1 gezeigt werden. Die Neuronen sind in Schichten organisiert. Die blauen Neuronen bilden die Eingangsschicht. Durch Erregung der Neuronen in der Eingangsschicht geben wir ein Signal in das Netz. Die Antwort des Netzes erhalten wir durch Beobachtung des Erregungszustandes der roten Neuronen (der Ergebnisschicht).

Bei einem Netz gibt es stets eine Eingangsschicht (die blauen Neuronen) und eine Ergebnisschicht (die roten Neuronen). Wenn wir mit dem Netz arbeiten, dann verändern wir den Zustand der blauen Neuronen und geben so ein Signal in das Netz hinein. Durch die Gruppierung der Neuronen in Schichten wandert das Signal dann durch das Netz zur roten Schicht. Wir lesen dort den Zustand der Neuronen ab. Der Zustand der roten Neuronen ist die Antwort des Netzes auf unser Eingangssignal. Wie wir sehen können sind die Neuronen einer Schicht nicht miteinander verbunden. Jedes Neuron einer Schicht ist mit allen Neuronen der nachfolgenden Schicht verbunden, aber es gibt keine Verbindungen kreuz und quer über mehrere Schichten hinweg. Die Erregungszustände und die Weiterleitung der Signale können wir also zwischen den Schichten in Tabellen notieren und behalten so den Überblick. In der Mathematik benutzt man sogenannte Matrizen dafür (eine Matrix ist ein Zahlenschema in Tabellenform, nur ohne Überschriften). Im Bild 2  seht Ihr 3 Neuronen pro Schicht. Das muss natürlich nicht so sein. Wir können beliebig viele Neuronen in den Schichten haben und die Anzahl muss nicht in allen Schichten gleich sein.

Damit das neuronale Netz lernt, was es lernen soll, zeigt man ihm viele Trainingsbeispiele, zum Beispiel Bilder von Hunden und Katzen. Für einen Computer bestehen Bilder aus Zahlen. Pro Bildpunkt sieht ein Computer drei Zahlen, je einen Intensitätswert für die Farbe Rot, Grün und Blau. Wenn Ihr ein Bild habt, das aus 1000 x 1000 Pixeln besteht, dann sind das 3 Millionen Zahlen. Für jedes dieser Zahlen könnte man z.B. ein eigenes Neuron in der Eingabeschicht haben. So kann man ein solches Bild dann in das neuronale Netz eingeben. Das Netz reagiert auf die Erregungen der Neuronen in der Eingabeschicht. Die Erregungen pflanzen sich entlang der Verbindungen zu den Neuronen der ersten inneren Schicht fort. Dort werden die Neuronen angeregt. Manche dieser Neuronen werden dann ein Signal erzeugen, manche nicht. Die Signale werden in die zweite Schicht weitergeleitet und so weiter. So wird das Eingangssignal verarbeitet bis es in der Ergebnisschicht ankommt, wo wir die Antwort des Netzes auf das Eingangssignal ablesen können. 

Wir zeigen dem Netz also Bilder von Hunden und Katzen und lesen die Antwort an der Ergebnisschicht ab. Im Lernprozess, zeigen wir dem Netz jetzt die richtige Antwort. Das Netz kann nun die Leitungsstärken der Verbindungen zwischen den Schichten so anpassen, dass es die richtige Antwort gibt (wie die Neuronen in Eurem Gehirn). Damit das Netz aber bei dem dritten Bild die Leitungsstärken nicht so anpasst, dass es zum Beispiel den Hund auf dem ersten Bild nicht mehr erkennt, gibt man ihm alle Beispiele auf einmal. Das Netz justiert dann die Leitungsstärken der Verbindungen zwischen den Schichten so, dass es möglichst viele der Bilder korrekt benennt.

Für die Justierung der Leitungsstärken im Netz benötigen ist ein Optimierungsprozess.  Ein Optimierungsprozess ist eine Prozedur, bei der sich das Netz verbessert und die wir sehr oft wiederholen können. Für neuronale Netze verwendet man dafür eine sogenannte Kostenfunktion. Das ist sehr typisch für Optimierungsprobleme. In einer Kostenfunktion messen wir einfach, wie weit weg wir von der richtigen Antwort sind. Sagen wir, wir möchten der Maschine beibringen zwei Zahlen zu multiplizieren und wir geben ihm zwei Beispiele:

1.   2⋅2=4
2.   3⋅3=9

Wie im letzten Abschnitt beschrieben, geben wir dem Netz die beiden Beispiele und lesen die Antworten, sagen wir y₁ und y₂, an der Ergebnisschicht ab. Eine Kostenfunktion mit der wir messen können wie weit wir von der richtigen Antwort entfernt sind wäre zum Beispiel

Die Antworten y₁ und y₂ hängen von den Leitungsstärken der Verbindungen zwischen den Schichten ab. Nehmen wir einfach mal an, das Netz hat nur zwei Leitungen mit Stärken a₁ und a₂. Dann können wir die Kostenfunktion schreiben als

Das ist im Prinzip das Gleiche wie oben, nur hier wird klar, dass C von den Stärken a₁ und a₂ abhängt. Die Kostenfunktion ist immer größer oder gleich null und null genau dann, wenn das Netz bei beiden Beispielen die richtige Antwort gegeben hat. Mit anderen Worten, diejenigen Leitungsstärken, die zur korrekten Antwort führen sind ein Minimum der Kostenfunktion. Wir benötigen jetzt also ein Verfahren, mit dem man Minima dieser Funktion findet. Die Ableitungen der Funktion C

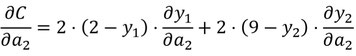
hängen von den Ableitungen der Funktionen y₁(a₁,a₂) und y₂(a₁,a₂) ab. Angenommen y₁(a₁,a₂) und y₂(a₁,a₂) wären Funktionen, die man einfach schriftlich differenzieren kann, dann könntet Ihr so ähnlich vorgehen, wie Ihr das in der Schule gelernt habt: d.h. Ableitungen bestimmen, Nullstellen finden und dann raussuchen welches der Nullstellen Minima sind. Leider ist das im Allgemeinen so nicht möglich. Wenn man so etwas nicht kann, gibt es approximative Verfahren wie zum Beispiel den sogenannten Gradientenabstieg. Man muss allerdings auch hier Ableitungen zumindest Näherungsweise bestimmen. Ableitungen zu approximieren kann sehr viel Rechenzeit benötigen, insbesondere in hohen Dimensionen. Erinnert Euch an der Bild mit 1000 x 1000 Bildpunkten. Hier haben wir 3 Millionen Eingabeneuronen und vielleicht einige Hundert Neuronen in den inneren Schichten. Eure Funktion hat also mehrere Millionen Variablen. Hier Ableitungen zu bestimmen kostet sehr viel Rechenzeit; das ist eines der Gründe, warum Neuronale Netze so lange ohne viel Beachtung in der Werkzeugkiste der Forscher schlummerten. Was man erst viel später nach der Entdeckung neuronaler Netze herausgefunden hat ist, das man die Ableitungen bei neuronalen Netzen sehr effizient ausrechnen kann, indem wir den Fehler den es gemacht hat an der Ergebnisschicht(!) wieder in das Netz führen und das Signal rückwärts durch das Netz laufen lassen. Warum das so funktioniert bedürfe einer längeren Erklärung und soll uns hier nicht weiter interessieren. Nur so viel: Der Grund, warum diese Methode funktioniert ist die Kettenregel (für Ableitungen), die Ihr aus der Schule kennt.

Die Verknüpfung zum Anfang ist, dass die benannten Probleme zu denjenigen gehören, die man schlecht in einer Liste von Anweisungen verpacken kann. Hinzu kommt, dass sich zum Beispiel bei Google-Anfragen das Nutzerverhalten laufend ändert und man also ein System benötigt, dass sich an dieses aktuelle Nutzerverhalten anpasst. Das lässt sich mit einer Liste von Anweisungen praktisch nicht realisieren. 

Ähnlich kann es bei Banken sein: Eine Bank könnte zum Beispiel ein System mit maschinellem Lernen so trainieren, dass es nahe an die Urteile der eigenen Experten herankommt. Mit einem solchen System kann die Bank dann ganz schnell tausende Unternehmen und Banken bewerten und diese Bewertungen dann ohne großen Aufwand neu erstellen, sobald sich irgendwelche Zahlen ändern. Das ist also ähnlich wie beim Schach oder dem Spiel Go. Spezialisierte Tätigkeiten lassen sich, sofern genügend Daten vorhanden sind und man genügend Zeit für die Entwicklung investiert, mit maschinellem Lernen sehr gut Computern beibringen. Manchmal werden die dann sogar besser als Menschen.

Autor:  Dr. Bijan Sahamie

Möchtet ihr mehr über den Arbeitgeber Bundesbank wissen? Dann klickt auf das Bild oder HIER.