Höhensatz und Kathetensatz im Dreieck
Hier erfahrt ihr alles zum Höhensatz und Kathetensatz, mit welchen ihr in rechtwinkligen Dreiecken rechnen könnt.
Höhensatz
Der Höhensatz besagt, dass das Quadrat der Höhe dasselbe ist, wie die beiden Teile der Hypotenuse, welche durch die Höhe geteilt werde, miteinander multipliziert. Also Folgendes:
Mit der Äquivalenzumformung könnt ihr die Formel natürlich auch nach p oder q auflösen, um diese zu berechnen.
Beispiel: Höhensatz berechnen
Ihr habt ein rechtwinkliges Dreieck mit den Längen für q=2cm und p=3cm. h berechnet ihr dann so:
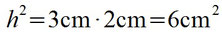
Jetzt nicht vergessen die Wurzel zu ziehen, da ihr ja h hoch 2 habt und dann habt ihr die länge von h:
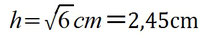
Kathetensatz
Mit dem Kathetensatz könnt ihr in rechtwinkligen Dreiecken die Längen a und b mit der Länge der Hypotenuse und den durch die Höhe geteilten Hälften der Hypotenuse berechnen. Dabei gilt, dass das Quadrat der Kathete dasselbe ist, wie der Teil der Hypotenuse, welche an der gesuchten Kathete liegt, mal die Hypotenuse, also:
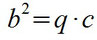
Mit der Äquivalenzumformung könnt ihr die Formel natürlich auch nach p oder q auflösen, um diese zu berechnen.
Beispiel: Kathetensatz berechnen
Ihr habt ein rechtwinkliges Dreieck, wie oben, mit den Längen p=2cm und c=8cm. Um a zu berechnen, geht ihr so vor:
Jetzt nicht vergessen die Wurzel zu ziehen, ihr möchtet ja nicht a quadrat wissen, sondern nur a:
Also ist a=4cm.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
