Kettenregel der Ableitung
Die Kettenregel ist eine der wichtigsten Regeln beim Ableiten. Diese ist nötig, wenn eine Funktion in einer anderen "drinnen steckt". Anhand der Beispiele werdet ihr genauer verstehen, wann dies der Fall ist. "Äußere Funktion abgeleitet, mal innere Funktion abgeleitet".
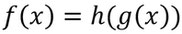

Tipp: Während ihr das Äußere ableitet, könnt ihr so tun als sei das Innere einfach ein x und leitet wie gewohnt ab (nur nicht vergessen anstatt x die innere Funktion aufzuschreiben).
Ausführliches Beispiel zur Kettenregel

Wenn ihr eine solche Funktion habt müsst ihr die Kettenregel anwenden, denn eine Funktion (2x) ist in einer anderen (sin(x)) „drinnen“. Bestimmt erstmal die innere und äußere Funktion.

Die innere Funktion ist 2x und die Äußere sin(x).

Geht jetzt nach der Formel vor, also leitet sin ab (lasst dabei die innere Funktion in der Äußeren stehen) und danach leitet ihr 2x ab und multipliziert das dann dahinter. Das ist dann die Ableitung.
Weitere Beispiele zur Anwendung der Kettenregel
Grün: äußere Funktion/Ableitung äußere Funktion
Blau: innere Funktion/Ableitung innere Funktion
Rot: innere Funktion immer in der Ableitung der Äußeren lassen!

Aufgaben zur Kettenregel
Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Übungsblätter downloaden. Lösungen zu den Aufgaben findet ihr dort ebenfalls:
